【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A.![]()
B.![]()
C.1
D.![]()
参考答案:
【答案】D
【解析】解:过F作FH⊥AE于H,
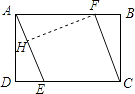
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE,
∴DE=BF,
∴AF=3﹣DE,
∴AE= ![]() ,
,
∵∠FHA=∠D=∠DAF=90°,
∴∠AFH+∠HAF=∠DAE+∠FAH=90°,
∴∠DAE=∠AFH,
∴△ADE∽△AFH,
∴ ![]() ,
,
∴AE=AF,
∴ ![]() =3﹣DE,
=3﹣DE,
∴DE= ![]() ,
,
所以答案是:D.
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转
 (0°<
(0°< <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为配合我市“富美乡村建设”宣传活动,某社区对“推动富美乡村建设的政策与举措的了解情况”进行问卷调查,问卷中把了解情况分为“非常了解(A)”、“有些了解(B)”、“不了解(C)”三类,并将调查结果分析整理后,制成如图所示的两个统计图.
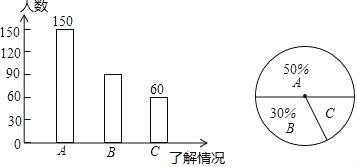
请根据以上两幅图的信息解答下列问题:
(1)这次调查活动共调查了_____人,其中“有些了解(B)”有_____人;
(2)在扇形统计图中,“B”所对应的扇形的圆心角度数是多少?
(3)如果该社区共有居民5000人,试估计“不了解(C)”的居民人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
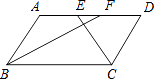
A.8
B.10
C.12
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)… 求证:这个二次函数的图象关于直线x=2对称,根据现有信息,题中的二次函数具有的性质:
(1 )过点(3,0)
(2 )顶点是(1,﹣2)
(3 )在x轴上截得的线段的长度是2
(4 )c=3a
正确的个数( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论错误的是( )
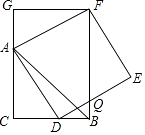
A.AC=FG
B.S△FAB:S四边形CBFG=1:2
C.AD2=FQAC
D.∠ADC=∠ABF -
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣
 ,﹣
,﹣ 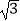 }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
相关试题

