【题目】某校在“校艺术节”期间,举办了A演讲,B唱歌,C书法,D绘画共四个项目的比赛,要求每位同学必须参加且限报一项,以九年(一)班为样本进行统计,并将统计结果绘制如下尚不完整的条形和扇形统计图,请根据统计图解答下列问题: 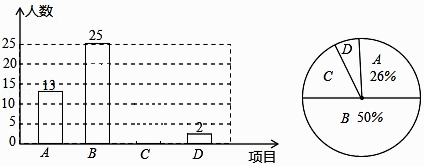
(1)在扇形统计图中,D项的百分率是多少?
(2)在扇形统计图中,C项的圆心角的度数是多少?
(3)请补充完整条形统计图;
(4)若该校九年级有500名学生,那么九年级参加演讲和唱歌比赛的学生共有多少人?
参考答案:
【答案】
(1)解:∵参加比赛的总人数为13÷26%=50人,
∴参加绘画比赛的学生人数占全班总人数的百分比是 ![]() ×100%=4%
×100%=4%
(2)解:根据题意得:
360°×(1﹣26%﹣50%﹣4%)=72°.
则参加书法比赛的C项所在的扇形圆心角的度数是72°
(3)解:参加书法的人数为50﹣(13+25+2)=10,补全图像如下:
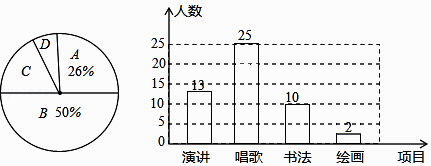
(4)解:∵500×(50%+26%)=380,
∴九年级参加演讲和唱歌比赛的学生约有380人
【解析】(1)根据A的人数及其百分比得出总人数,绘画人数除50即可.(2)两图结合,按频数和频率的关系知c=20%,由此即可求出相应圆心角的度数;(3)总人数减去其余各组人数得出C组人数,即可补全图形;(3)利用样本估计总体即可.
【考点精析】通过灵活运用扇形统计图和条形统计图,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等边△ABC沿着DE折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则AD的长为( )
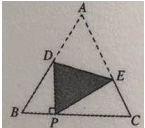
A. 5 B. 3 C. 4
 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣2与反比例函数y=
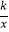 的图像交于点A(3,1)和点B.
的图像交于点A(3,1)和点B. 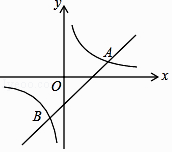
(1)求k的值及点B的坐标;
(2)若点P是坐标平面内一点,且以A,O,B,P为顶点构成一个平行四边形,请你直接写出该平行四边形对角线交点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转使CD边恰好过AB的中点O,得到△D1CE1如图(2),则线段AD1的长度为( )

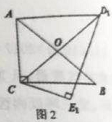
A. 3
 B. 5 C. 4 D.
B. 5 C. 4 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在一张长方形纸条上画一条数轴.
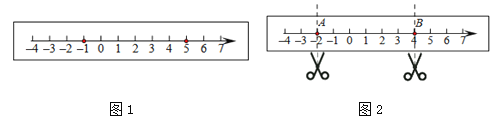
(1)折叠纸条使数轴上表示
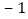 的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
的点与表示5的点重合,折痕与数轴的交点表示的数是 ;(2)如果数轴上两点之间的距离为8,经过(1)的折叠方式能够重合,那么左边这个点表示的数是 ;
(3)如图2,点A、B表示的数分别是
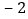 、
、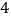 ,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;(4)如图2,若将此纸条沿A、B两处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折
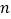 次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含
次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含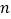 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
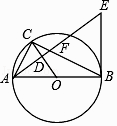
(1)求证:BE是⊙O的切线;
(2)若CD=1,cos∠AEB=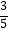 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

