【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A. ![]() B.
B.  C.
C.  D.
D. 
参考答案:
【答案】C
【解析】
日历中的每个数都是整数且上下相邻是7,左右相邻相差是1根据题意可列方程求解.
解:A、b=a+7,c=b+7=a+14,
∵a+b+c=39,
∴a+a+7+a+14=39,解得a=6;
B、b=a+1+7=a+8,c=b+1+7=a+16,
∵a+b+c=39,
∴a+a+8+a+16=39,解得a=5;
C、b=a-1+7=a+6,c=b+1=a+7,
∵a+b+c=39,
∴a+a+6+a+7=39,解得a=![]() ;
;
D、b=a+7,c=b+1=a+8,
∵a+b+c=39,
∴a+a+7+a+8=39,解得a=8.
由题可知,a、b、c均为整数,
所以本题选择C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“校艺术节”期间,举办了A演讲,B唱歌,C书法,D绘画共四个项目的比赛,要求每位同学必须参加且限报一项,以九年(一)班为样本进行统计,并将统计结果绘制如下尚不完整的条形和扇形统计图,请根据统计图解答下列问题:
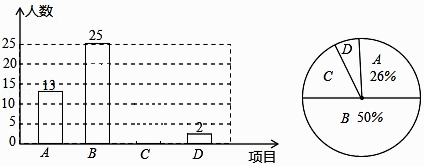
(1)在扇形统计图中,D项的百分率是多少?
(2)在扇形统计图中,C项的圆心角的度数是多少?
(3)请补充完整条形统计图;
(4)若该校九年级有500名学生,那么九年级参加演讲和唱歌比赛的学生共有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在一张长方形纸条上画一条数轴.
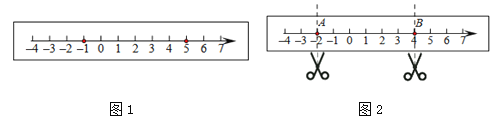
(1)折叠纸条使数轴上表示
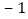 的点与表示5的点重合,折痕与数轴的交点表示的数是 ;
的点与表示5的点重合,折痕与数轴的交点表示的数是 ;(2)如果数轴上两点之间的距离为8,经过(1)的折叠方式能够重合,那么左边这个点表示的数是 ;
(3)如图2,点A、B表示的数分别是
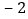 、
、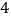 ,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;
,数轴上有点C,使得AC=2BC,那么点C表示的数是 ;(4)如图2,若将此纸条沿A、B两处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折
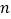 次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含
次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含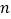 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
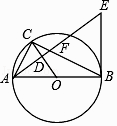
(1)求证:BE是⊙O的切线;
(2)若CD=1,cos∠AEB=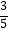 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x+3(2x﹣3)=12﹣(x﹣4)
(2)
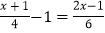
(3)
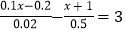
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从今年1月1日起调整居民用水价格,每立方米水费上涨
 ,小丽家去年12月的水费是15元,而今年7月的水费则是30元.已知小丽家今年7月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格.请表述出此题的主要等量关系,(写出一个即可)_____________.
,小丽家去年12月的水费是15元,而今年7月的水费则是30元.已知小丽家今年7月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格.请表述出此题的主要等量关系,(写出一个即可)_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a<0,c>0)与x轴交于A,B两点,与y轴交于点C,其对称轴l为x=﹣1,直线y=kx+m经过A,C两点,与抛物线的对称轴l交于点D,且AD=2CD,连接BC,BD.
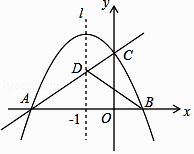
(1)求A,B两点的坐标;
(2)求证:a=﹣k;
(3)若△BCD是直角三角形,求抛物线的解析式.
相关试题

