【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.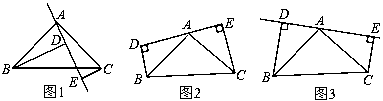
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
参考答案:
【答案】
(1)解:在△ABD和△CAE中,
∵∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAD=∠ABD.
又∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.又AE=AD+DE,∴AE=DE+CE,即BD=DE+CE
(2)解:BD=DE﹣CE.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.又AB=AC,∠ADB=∠CEA=90°,∴△ADB≌△CEA.∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,即 BD=DE﹣CE
(3)解:同理:BD=DE﹣CE
【解析】(1)根据已知条件证明△ABD≌△CAE,可得BD=AE,AD=CE,则结论可得;(2)关系是:BD=DE﹣CE,证明方法同(1);(3)同理:BD=DE﹣CE。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算 x 2 y 2 _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1.
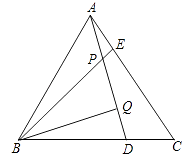
(1)求证:∠BPQ=60°(提示:利用三角形全等、外角的性质)
(2)求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个角为70゜,则其顶角的度数为_____ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知5x=36,5y=2,求5x﹣2y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是
 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )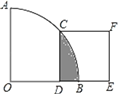
A. 2π﹣8 B. 4π﹣8 C. 2π﹣4 D. 4π﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值: 4 x 12 2x 32x 3 ,其中 x 1.
相关试题

