搜索
【题目】如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点A1(﹣1，1)，第二次向右跳动3个单位至点A2(2，1)，第三次跳动至点A3(﹣2，2)，第四次向右跳动5个单位至点A4(3，2)，…，以此规律跳动下去，点A第2020次跳动至点A2020的坐标是( )
A.(1012，1011)B.(1009，1008)
C.(1010，1009)D.(1011，1010)
参考答案：
【答案】D
【解析】
根据点的坐标、坐标的平移寻找规律即可求解．
解：由题意可知：A1（-1，1），A2（2，1）A3（-2，2）A4（3，2）A5（-3）3 A6（4，3）A7（-4，4）A8（5，4）…
∴A2n-1（-n，n） A2n（n+1，n）（n为正整数）
所以2n=2020，
解得n=1010
所以A2020（1011，1010）
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
A. 4B. 3C. 2D. 1
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm／s。
⑴连接AQ、CP交于点M，在点P、Q运动的过程中，∠CMQ的大小变化吗？若变化，则说明理由，若不变，请直接写出它的度数；
⑵点P、Q在运动过程中，设运动时间为t，当t为何值时，△PBQ为直角三角形？
⑶如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ的大小变化吗？则说明理由；若不变，请求出它的度数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：如图，分别以△ABC的两边AB和AC为边向外作正方形ABMN和正方形ACDE，CN、BE交于点P. 求证：∠ANC = ∠ABE.
应用：Q是线段BC的中点，连结PQ. 若BC = 6，则PQ = ___________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.
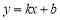一定是一次函数B. 有的实数在数轴上找不到对应的点
C. 长为
的三条线段能组成直角三角形D. 无论
为何值，点
总是在第二象限 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．
（1）求抛物线的解析式；
（2）若MN与直线y=﹣2
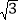x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：①求证：BC平分∠MBN；
②求△MBC外心的纵坐标的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点
，分别根据下列条件求出点P的坐标.（1）点P在x轴上；
（2）点P在y轴上；
（3）点P到x轴、y轴的距离相等；
（4）点Q的坐标为
，直线
轴.
相关试题
