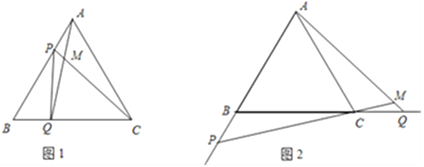
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

参考答案:
【答案】见解析
【解析】试题分析:(1)因为点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,所以AP=BQ.AB=AC,∠B=∠CAP=60°,因而运用边角边定理可知△ABQ≌△CAP.再用全等三角形的性质定理及三角形的角间关系、三角形的外角定理,可求得CQM的度数;
(2)设时间为t,则AP=BQ=t,PB=4-t.分别就①当∠PQB=90°时;②当∠BPQ=90°时利用直角三角形的性质定理求得t的值;
(3)首先利用边角边定理证得△PBC≌△QCA,再利用全等三角形的性质定理得到∠BPC=∠MQC.再运用三角形角间的关系求得∠CMQ的度数.
试题解析:(1)∠CMQ不变.
AC="BA," ∠A=∠B, AP="BQ,"
∴△ACP≌△BAQ, ∴∠ACP=∠BAQ,
∴∠CMQ=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC=60°.
∴∠CMQ恒等于60°,不发生变化.
(2)设运动了t秒
当△PBQ为Rt三角形时 ∠B="60°"
①当∠BPQ=30°时 ∴PB="AB-BP=4-t=2BQ=2t" 解得t=![]()
②当∠PQB=30°时 则BQ=t=2PB=2(AB-AP)=2(4-t) 解得t=![]()
(3)∠CMQ不变.
∵AC=CB,∠ACQ=120°=∠CBP, CQ="BP,"
∴△ACQ≌△CBP, ∴∠CAQ=∠BCP,
∴∠CMQ=∠CAQ+∠ACM=∠BCP+∠ACM=∠MCQ+∠ACM=∠ACQ=120°.
∴∠CMQ恒等于120°,不会发生变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过13小时的节气是( )

A.惊蛰
B.小满
C.秋分
D.大寒 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.下面四个推断:

①2009年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是4032亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入增长的平均数比2013年到2015年技术收入增长的平均数大.
其中,正确的是( )
A.①③
B.①④
C.②③
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )
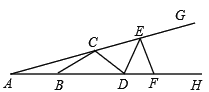
A. 80° B. 90° C. 100° D. 108°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“作三角形一边中线”的尺规作图过程. 已知:△ABC(如图1),求作:BC边上的中线AD.
作法:如图2,
(i)分别以点B,C为圆心,AC,AB长为半径作弧,两弧相交于P点;
(ii)作直线AP,AP与BC交于D点.
所以线段AD就是所求作的中线.
请回答:该作图的依据是 .
相关试题

