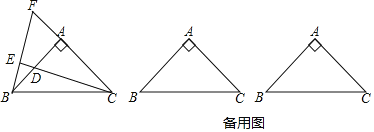
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.
参考答案:
【答案】(1)证明见解析;(2)见解析.
【解析】
(1)易证∠FBA=∠FCE,结合条件容易证到△FAB≌△DAC,从而有FA=DA,就可得到AB=AD+BD=FA+BD.
(2)由于点D的位置在变化,因此线段AF、BD、AB之间的大小关系也会相应地发生变化,只需画出图象并借鉴(1)中的证明思路就可解决问题.
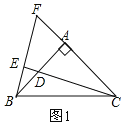
(1)如图1,∵BE⊥CD,即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
∵AB=AC,
∴△FAB≌△DAC.
∴FA=DA.
∴AB=AD+BD=FA+BD.
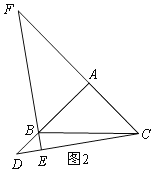
(2)如图2,当D在AB延长线上时,AF=AB+BD,
理由是:同理得:△FAB≌△DAC,
∴AF=AD=AB+BD;
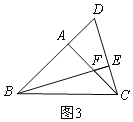
如图3,当D在AB反向延长线上时,BD=AB+AF,
理由是:同理得:△FAB≌△DAC,
∴AF=AD,
∴BD=AB+AD=AB+AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是一个聪明而又富有想象力的孩子.学习了“有理数的乘方”后,他就琢磨着使用“乘方”这一数学知识脑洞大开地定义出“有理数的除方”概念.于是规定:若干个相同有理数(均不能为0)的除法运算叫做除方,如5÷5÷5,(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)等,类比有理数的乘方.小明把5÷5÷5记作f(3,5),(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)记作f(4,﹣2)
(1)直接写出计算结果,f(5,
 )= ,f(6,3)= ;
)= ,f(6,3)= ;(2)关于“有理数的除方”下列说法正确的是 (填序号)
①对于任何正整数n,都有f(n,﹣1)=1;
②f(6,3)=f(3,6);
③f(2,a)=1(a≠0);
④对于任何正整数n,都有f(2n,a)<0(a<0).
(3)小明深入思考后发现:“除方”运算能够转化成乘方运算,且结果可以写成幂的形式.请推导出“除方”的运算公式f(n,a)(n为正整数,a≠0,n≥2),要求写出推导过程将结果写成幂的形式(结果用含a,n的式子表示)
(4)请利用(3)问的推导公式计算:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形
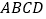 中,
中, ,
,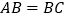 .
.(1)如图1.连接
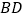 ,若
,若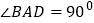 ,求证:
,求证: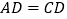 .
.(2)如图2,点
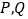 分别在线段
分别在线段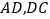 上,满足
上,满足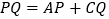 ,求证:
,求证: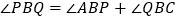 ;
;(3)若点
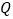 在
在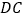 的延长线上,点
的延长线上,点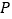 在
在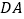 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足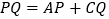 ,请写出
,请写出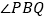 与
与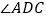 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.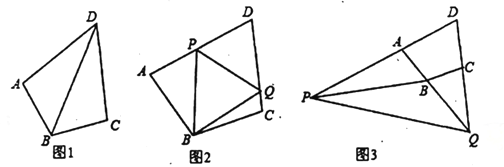
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B、C、D四点所表示的数分别是a、b、c、d,且(a+16)2+(d+12)2=﹣|b﹣8|﹣|c﹣10|.
(1)求a、b、c、d的值;
(2)点A,B沿数轴同时出发相向匀速运动,4秒后两点相遇,点B的速度为每秒2个单位长度,求点A的运动速度;
(3)A,B两点以(2)中的速度从起始位置同时出发,向数轴正方向运动,与此同时,C点以每秒1个单位长度的速度向数轴正方向开始运动,若t秒时有2AB=CD,求t的值;
(4)A,B两点以(2)中的速度从起始位置同时出发,相向而行当A点运动到C点时,迅速以原来速度的2倍返回,到达出发点后,保持改变后的速度又折返向C点运动;当B点运动到A点的起始位置后停止运动.当B点停止运动时,A点也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段a和射线OA,射线OA上有点B.

(1)用圆规和直尺在射线OA上作线段CD,使点B为CD的中点,点C在点B的左边,且BC=a.(不用写作法,保留作图痕迹)
(2)在(1)的基础上,若OB=12cm,OC=5cm,求线段OD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
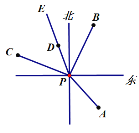
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

相关试题

