【题目】如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
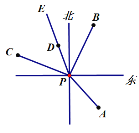
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
参考答案:
【答案】(1)160°;(2)轮船D在灯塔P北偏西20°的方位上
【解析】
(1)先求出∠BPC的度数,根据角平分线的定义,得∠BPE的度数,再求出∠APB的度数,进而即可求解;
(2)求出∠MPD的度数,进而即可求解.
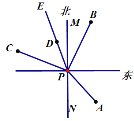
(1)∵∠NPA = 40°, ∠MPB = 30°,∠MPC = 70°,
∴∠BPC = ∠MPB + ∠MPC = 30°+70°= 100°,
∵PE平分∠BPC,
∴∠BPE =![]() ∠BPC =
∠BPC =![]() ×100°=50°,
×100°=50°,
∴∠APB =180°-∠NPA-∠MPB = 180°-40°-30°=110°,
∴∠APE = ∠BPE + ∠APB = 50°+ 110°= 160° ,
(2)∵∠MPD = ∠BPE -∠MPB = 50°-30°= 20°,
∴轮船D在灯塔P北偏西20°的方位上 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B、C、D四点所表示的数分别是a、b、c、d,且(a+16)2+(d+12)2=﹣|b﹣8|﹣|c﹣10|.
(1)求a、b、c、d的值;
(2)点A,B沿数轴同时出发相向匀速运动,4秒后两点相遇,点B的速度为每秒2个单位长度,求点A的运动速度;
(3)A,B两点以(2)中的速度从起始位置同时出发,向数轴正方向运动,与此同时,C点以每秒1个单位长度的速度向数轴正方向开始运动,若t秒时有2AB=CD,求t的值;
(4)A,B两点以(2)中的速度从起始位置同时出发,相向而行当A点运动到C点时,迅速以原来速度的2倍返回,到达出发点后,保持改变后的速度又折返向C点运动;当B点运动到A点的起始位置后停止运动.当B点停止运动时,A点也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
-
科目: 来源: 题型:
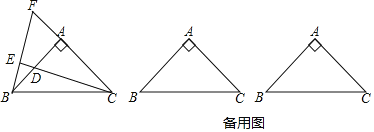
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段a和射线OA,射线OA上有点B.

(1)用圆规和直尺在射线OA上作线段CD,使点B为CD的中点,点C在点B的左边,且BC=a.(不用写作法,保留作图痕迹)
(2)在(1)的基础上,若OB=12cm,OC=5cm,求线段OD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

-
科目: 来源: 题型:
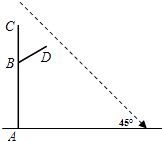
查看答案和解析>>【题目】如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短
 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程
如图,OA、BC分别是普通列车和动车从盐城开往北京的路程 与时间
与时间 的函数图象
的函数图象 请根据图中的信息,解答下列问题:
请根据图中的信息,解答下列问题: 根据图象信息,普通列车比动车早出发______h,动车的平均速度是______
根据图象信息,普通列车比动车早出发______h,动车的平均速度是______ ;
; 分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
分别求出OA、BC的函数表达式,并写出自变量x的取值范围; 动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
相关试题

