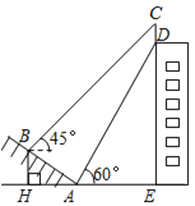
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
参考答案:
【答案】(1)5;(2)2.7m.
【解析】试题分析:(1)过B作DE的垂线,设垂足为G.分别在Rt△ABH中,通过解直角三角形求出BH、AH;
(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE-DE即可求出宣传牌的高度.
试题解析:(1)过B作BG⊥DE于G,
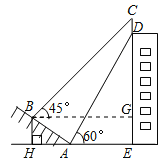
Rt△ABH中,i=tan∠BAH=![]() ,
,
∴∠BAH=30°,
∴BH=![]() AB=5;
AB=5;
(2)∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵由(1)得:BH=5,AH=5![]() ,
,
∴BG=AH+AE=5![]() +15,
+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5![]() +15.
+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=![]() AE=15
AE=15![]() .
.
∴CD=CG+GE-DE=5![]() +15+5-15
+15+5-15![]() =20-10
=20-10![]() ≈2.7m.
≈2.7m.
答:宣传牌CD高约2.7米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义某种新运算:对于任意两个有理数a、b,有a*b=a2﹣2b+1,例如:2*3=22﹣2×3+1=﹣1.
(1)计算:3*(﹣2)的值;
(2)试化简:x*(x2+1).
-
科目: 来源: 题型:
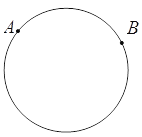
查看答案和解析>>【题目】如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点 (备注:圆形轨道上两点的距离是指圆上这两点间较短部分展直后的线段长).动点P从A点出发,以a cm/s的速度,在轨道上按逆时针方向运动,与此同时,动点Q从B出发,以3 cm/s的速度,按同样的方向运动.设运动时间为t (s),当t = 5时,动点P、Q第一次相遇.
(1)求a的值;
(2)若a > 3,在P、Q第二次相遇前,当动点P、Q在轨道上相距12cm时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)共随机调查了名学生,课外阅读时间在6﹣8小时之间有人,并补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)请估计该校3000名学生每周的课外阅读时间不小于6小时的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.
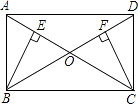
求证:
(1)∠ACB=∠DBC;
(2)BE=CF. -
科目: 来源: 题型:
查看答案和解析>>【题目】某办公用品销售商店推出两种优惠方法:甲种:购1个书包,赠送1支水性笔;乙种:购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包和水性笔x支(x≥4).
(1)用含x的式子分别表示两种优惠方法购买所需的费用;
(2)求购买多少支水笔时,用两种优惠方法购买所需的费用一样多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x﹣2的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
相关试题

