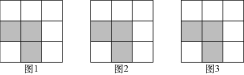
【题目】下列3×3的网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)请在图1中选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)请在图2中选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)请在图3中选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据轴对称定义,在最上一行中间一列涂上阴影即可;
(2)根据中心对称定义,在最下一行、最右一列涂上阴影即可;
(3)在最上一行、中间一列,中间一行、最右一列涂上阴影即可.
(1)如图1所示;

(2)如图2所示;
(3)如图3所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE
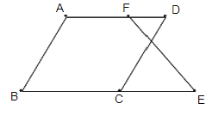
证明:∵∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知 ),
∴___________ (等量代换)
∴ ∥
∴∠E=∠DFE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
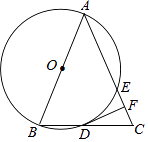
(1)求证:DF是⊙O的切线;
(2)若AE=4,cosA=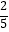 ,求DF的长.
,求DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】贵阳市“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3)
0.3
0.4
0.5
0.6
0.7
家庭数(个)
2
2
4
1
1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5
B.0.5和0.5
C.0.47和4
D.0.5和4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3 , 若S1=3,S3=9,则S2的值为( )

A.12
B.18
C.24
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2﹣4ac>0;④﹣
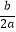 <0,正确的是( )
<0,正确的是( )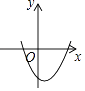
A.①②
B.②④
C.①③
D.③④ -
科目: 来源: 题型:
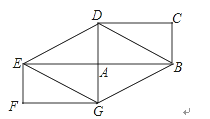
查看答案和解析>>【题目】如图,矩形ABCD和矩形AEFG关于点A中心对称,
(1)四边形BDEG是菱形吗?请说明理由.
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
相关试题

