【题目】已知M、N直线l上两点,MN=20,O、P为线段MN上两动点,过O、P分别作长方形OABC与长方形PDEF(如图),其中,两边OA、PF分别在直线l上,图形在直线l的同侧,且OA=PF=4,CO=DP=3,动点O从点M出发,以1单位/秒的速度向右运动;同时,动点P从点N出发,以2单位/秒的速度向左运动,设运动的时间为t秒.
(1)若t=2.5秒,求点A与点F的距离;
(2)求当t为何值时,两长方形重叠部分为正方形;
(3)运动过程中,在两长方形没有重叠部分前,若能使线段AB、BC、AF的长构成三角形,求t的取值范围.

参考答案:
【答案】(1)4.5;(2)当t分别为5秒、![]() 秒时,两长方形重叠部分为正方形;(3)t的取值范围为
秒时,两长方形重叠部分为正方形;(3)t的取值范围为![]()
【解析】
(1)求出MA,NF的值即可判断;
(2)分两种情形:ABEF是正方形;OCDP是正方形.分别求解即可解决问题;
(3)求出相遇前AF=7或1时的时间即可解决问题.
解:(1)当t=2.5秒时,MA=MO+OA=2.5+4=6.5,
NF=NP+PF=2.5×2+4=9,
∴AF=20﹣6.5﹣9=4.5.
(2)第一次重叠部分为正方形ABEF(如图)此时FA=3,
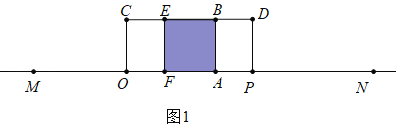
MA=t+4,NF=2t+4,
∴(t+4)+(2t+4)﹣20=3,
∴t=5.
第二次重叠部分为正方形PDCO(如图)此时OP=3,
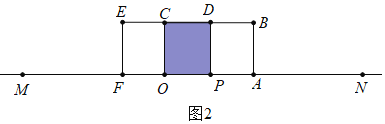
OM=t,PN=2t,
∴20﹣t﹣2t=3,
∴t=![]() ,
,
∴当t分别为5秒、![]() 秒时,两长方形重叠部分为正方形;
秒时,两长方形重叠部分为正方形;
(3)∵线段AB、BC、AF的长构成三角形,AB=3,BC=4,
∴1<AF<7,
重叠前AF=7,则有20﹣(t+4)﹣(2t+4)=7,
解得t=![]() ;
;
AF=1,则有20﹣(t+4)﹣(2t+4)=1,
解得t=![]() ,
,
∴t的取值范围为![]() .
.
-
科目: 来源: 题型:
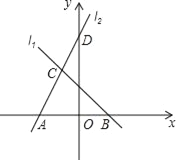
查看答案和解析>>【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法)
(1)以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出B1的坐标;
(2)再把△A1B1C1绕点C1 顺时针旋转90°,得到△A2B2C1,请你画出△A2B2C1,并写出B2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点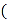 点D不与B,C重合
点D不与B,C重合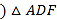 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF. 如图1,求证:
如图1,求证: ≌
≌ ;
;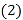 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;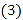 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问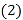 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.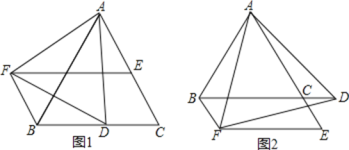
-
科目: 来源: 题型:
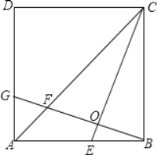
查看答案和解析>>【题目】如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
(1)证明:BE=AG;
(2)E位于什么位置时,∠AEF=∠CEB?说明理由.
-
科目: 来源: 题型:
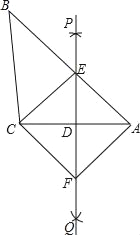
查看答案和解析>>【题目】已知:如图,在△ABC中,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:四边形AECF是菱形;
(2)若AD=3,AE=5,则求菱形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,王同学使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
 ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.
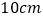 B.
B. 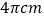 C.
C. 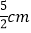 D.
D. 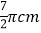
相关试题

