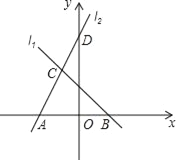
【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.
参考答案:
【答案】(1)C(﹣1,3),直线l2的解析式为y=2x+5;(2)△ABC的面积为![]() .
.
【解析】
试题(1)由题意把点C(-1,m)的坐标代入y=-x+2即可求得m的值,再结合直线l2经过点D(0,5)即可根据待定系数法求得直线l2的解析式;
(2)先分别求得两条直线与x轴的交点坐标,再根据三角形的面积公式即可求得结果.
(1)在y=-x+2中,当![]() 时,
时,![]()
∴点C的坐标为(-1,3)
设直线l2的解析式为![]()
∵图象过点C(-1,3),D(0,5)
∴![]() ,解得
,解得![]()
∴直线l2的解析式为![]() ;
;
(1)在y=-x+2中,当![]() 时,
时,![]() ,
,![]() ,即A点坐标为(2,0)
,即A点坐标为(2,0)
在![]() 中,当
中,当![]() 时,
时,![]() ,
,![]() ,即A点坐标为(
,即A点坐标为(![]() ,0)
,0)
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
我们给出如下定义:数轴上给定两点
 ,
, 以及一条线段
以及一条线段 ,若线段
,若线段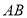 的中点
的中点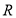 在线段
在线段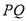 上(点
上(点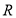 可以与点
可以与点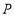 或
或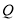 重合),则称点
重合),则称点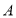 与点
与点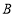 关于线段
关于线段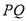 径向对称.下图为点
径向对称.下图为点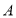 与点
与点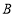 关于线段
关于线段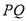 径向对称的示意图.
径向对称的示意图.
解答下列问题:
如图1,在数轴上,点
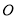 为原点,点
为原点,点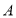 表示的数为-1,点
表示的数为-1,点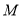 表示的数为2.
表示的数为2.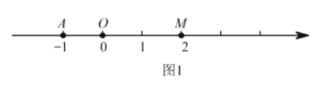
(1)①点
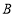 ,
,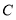 ,
,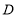 分别表示的数为-3,
分别表示的数为-3,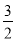 ,3,在
,3,在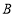 ,
,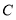 ,
,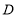 三点中, 与点
三点中, 与点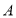 关于线段
关于线段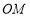 径向对称;
径向对称;②点
 表示的数为
表示的数为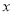 ,若点
,若点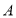 与点
与点 关于线段
关于线段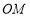 径向对称,则
径向对称,则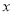 的取值范围是 ;
的取值范围是 ;(2)在数轴上,点
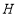 ,
,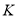 ,
,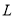 表示的数分别是-5,-4,-3,当点
表示的数分别是-5,-4,-3,当点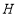 以每秒1个单位长度的速度向正半轴方向移动时,线段
以每秒1个单位长度的速度向正半轴方向移动时,线段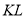 同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为
同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为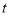 (
(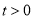 )秒,问
)秒,问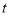 为何值时,线段
为何值时,线段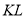 上至少存在一点与点
上至少存在一点与点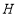 关于线段
关于线段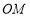 径向对称.
径向对称. -
科目: 来源: 题型:
查看答案和解析>>【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将
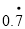 化成分数.
化成分数.解:设
 .
.方程两边都乘以10,可得
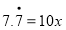 .
.由
 和
和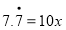 ,可得
,可得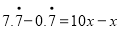 即
即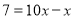 .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)解得
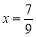 ,即
,即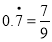 .
.填空:将
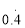 写成分数形式为 .
写成分数形式为 .(2)请你仿照上述方法把小数
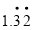 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
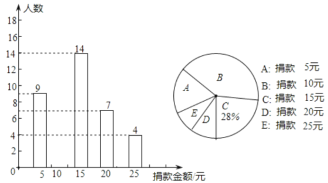
(1)本次共抽查学生多少人?并将条形统计图补充完整;
(2)请直接写出捐款金额的众数和中位数,并计算捐款的平均数;
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江夏区某出租车在某一天以江夏体育馆为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9,-2,-5,-4,-12,+8,+3,-1,-4,+10
(1)将最后一名乘客送到目的地,出租车离江夏体育馆出发点多远?
(2)直接写出该出租车在行驶过程中,离江夏体育馆最远的距离是______.
(3)出租车按物价部门规定,行程不超过3km的(含3km),按起步价8元收费,若行程超过3km的,则超过的部分,每千米加收1.2元,该司机这天的营业额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数:

(1)第①行的第n个数是_______(直接写出答案,n为正整数)
(2)第②、③行的数与第①行相对应的数分别有什么关系?
(3)取每行的第9个数,记这三个数的和为a,化简计算求值:(5a2-13a-1)-4(4-3a+
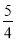 a2)
a2)
相关试题

