【题目】如图,抛物线y=ax2+ ![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).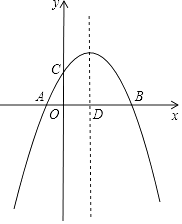
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
参考答案:
【答案】
(1)
解:由题意  ,
,
解得 ![]() ,
,
∴二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:存在.如图1中,
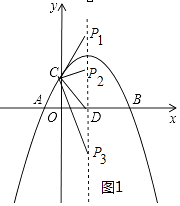
∵C(0,2),D( ![]() ,0),
,0),
∴CD= ![]() =
= ![]() ,
,
当CP=CD时,P1( ![]() ,4),
,4),
当DP=DC时,P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() ).
).
综上所述,满足条件的点P坐标为( ![]() ,4)或(
,4)或( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]()
(3)
解:如图2中,作CM⊥EF于M,

∵B(4,0),C(0,2),
∴直线BC的解析式为y=﹣ ![]() ,设E(a,﹣
,设E(a,﹣ ![]() +2),F(a,﹣
+2),F(a,﹣ ![]() a2+
a2+ ![]() a+2),
a+2),
∴EF=﹣ ![]() a2+
a2+ ![]() a+2﹣(﹣
a+2﹣(﹣ ![]() +2)=﹣
+2)=﹣ ![]() a2+2a,(0≤a≤4),
a2+2a,(0≤a≤4),
∵S四边形CDBF=S△BCD+S△CEF+S△BEF= ![]() BDOC+
BDOC+ ![]() EFCM+
EFCM+ ![]() EFBN
EFBN
= ![]() +
+ ![]() a(﹣
a(﹣ ![]() a2+2a)+
a2+2a)+ ![]() (4﹣a)(﹣
(4﹣a)(﹣ ![]() a2+2a)
a2+2a)
=﹣a2+4a+ ![]()
=﹣(a﹣2)2+ ![]() ,
,
∴a=2时,四边形CDBF的面积最大,最大值为 ![]() ,
,
∴E(2,1)
【解析】(1)利用待定系数法转化为解方程组即可.(2)如图1中,分两种情形讨论①当CP=CD时,②当DP=DC时,分别求出点P坐标即可.(3)如图2中,作CM⊥EF于M,设E(a,﹣ ![]() +2),F(a,﹣
+2),F(a,﹣ ![]() a2+
a2+ ![]() a+2),则EF=﹣
a+2),则EF=﹣ ![]() a2+
a2+ ![]() a+2﹣(﹣
a+2﹣(﹣ ![]() +2)=﹣
+2)=﹣ ![]() a2+2a,(0≤a≤4),根据S四边形CDBF=S△BCD+S△CEF+S△BEF=
a2+2a,(0≤a≤4),根据S四边形CDBF=S△BCD+S△CEF+S△BEF= ![]() BDOC+
BDOC+ ![]() EFCM+
EFCM+ ![]() EFBN,构建二次函数,利用二次函数的性质即可解决问题.
EFBN,构建二次函数,利用二次函数的性质即可解决问题.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复

 下表是活动中的一组统计数据:
下表是活动中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请你设计一个增(减)袋中白球或黄球球个数的方案,使得从袋中摸出一个球,这只球是黄球的概率大于是白球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式
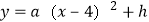 ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a=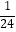 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为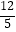 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,S△ADE=8,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.

(1)求证:DE是⊙O的切线;
(2)当AB=4 ,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
,∠C=30°时,求图中阴影部分的面积(结果保留根号和π). -
科目: 来源: 题型:
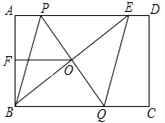
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF =4,求菱形BPEQ的周长.
相关试题

