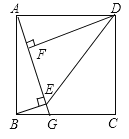
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,S△ADE=8,求EF的长.

参考答案:
【答案】(1)见解析;(2)3
【解析】分析:(1)由∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,推出∠BAE=∠ADF,即可根据AAS证明△ABE≌△DAF;
(2)设EF=x,则AE=DF=x+1,根据S△ADE=8,列出方程即可解决问题.
详解:(1)∵四边形ABCD是正方形,∴AB=AD.
∵DF⊥AG,BE⊥AG,∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,∴∠BAE=∠ADF.在△ABE和△DAF中,∵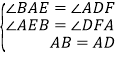 ,∴△ABE≌△DAF(AAS).
,∴△ABE≌△DAF(AAS).
(2)设EF=x,则AE=DF=x+1.
由S△ADE=8,得:![]() (x+1)2=8,
(x+1)2=8,
解得:x=3或﹣5(舍弃),∴EF=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式
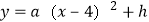 ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a=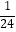 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为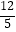 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+
 x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).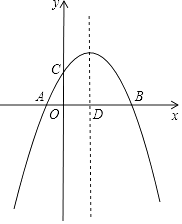
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.

(1)求证:DE是⊙O的切线;
(2)当AB=4 ,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
,∠C=30°时,求图中阴影部分的面积(结果保留根号和π). -
科目: 来源: 题型:
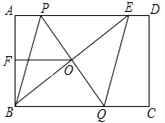
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF =4,求菱形BPEQ的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线
 相交于点
相交于点 于点
于点 于点F,连结
于点F,连结 ,则下列结论:
,则下列结论: ;
; ;
; ;
; 图中共有四对全等三角形
图中共有四对全等三角形 其中正确结论的个数是
其中正确结论的个数是

A. 4 B. 3 C. 2 D. 1
相关试题

