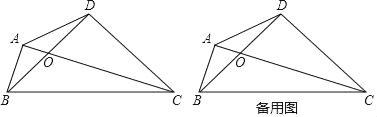
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,OB=OD,BD=CD,∠BAC=∠BDC=90°.
(1)填空:∠ABD=∠ ;
(2)求![]() 的值;
的值;
(3)点D关于直线BC的对称点为N,连接AN,请补全图形,探究线段AN,AD有怎样的关系,并加以证明.
参考答案:
【答案】(1)ACD;(2)![]() ;(3)AD⊥AN,
;(3)AD⊥AN,![]() .
.
【解析】
(1)因为∠BAC=∠BDC=90°,得到∠ABD+∠AOB=90°,∠ACD+∠COD=90°,根据等角的余角相等,即可得到∠ABD=∠ACD.
(2)作DH⊥OC于H.证明△BAO≌△DHO,根据全等三角形的性质得到AB=DH,设OD=OB=a,则BD=CD=2a,根据等面积法求出DH的长度,即可求出![]() 的值;
的值;
(3)连接BN、CN.根据△BDC是等腰直角三角形,得到D、N关于BC对称,有O′A=O′D=O′N=O′B=O′C,得到A、B、N、C、D五点共圆,根据圆周角定理得到∠AND=∠ACD,即可求出![]()
解:(1)∵∠BAC=∠BDC=90°,
∴∠ABD+∠AOB=90°,∠ACD+∠COD=90°,
∵∠AOB=∠COD,
∴∠ABD=∠ACD.
故答案为ACD.
(2)作DH⊥OC于H.
∵∠BAO=∠DHO=90°,∠AOB=∠DOH,OB=OD,
∴△BAO≌△DHO,
∴AB=DH,设OD=OB=a,则BD=CD=2a,![]()
∴![]()
(3)结论:AD⊥AN, ![]()
理由:连接BN、CN.
∵△BDC是等腰直角三角形,
D、N关于BC对称,
∴四边形DBNC是正方形,设BC的中点为O′,连接O′N、O′A、O′D.
则有O′A=O′D=O′N=O′B=O′C,
∴A、B、N、C、D五点共圆,
∵DN是⊙O′的直径,
∴∠DAN=90°,
∴AD⊥AN,
∵∠AND=∠ACD,
∴tan∠AND=tan∠ACD,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=
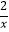 (x>0)相交于P(1,m).
(x>0)相交于P(1,m). 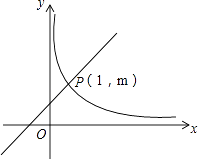
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,求点Q的坐标为
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.

(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B
(1)求直线l的表达式;
(2)若点B的横坐标是1,求关于x、y的方程组
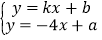 的解及a的值.
的解及a的值.(3)若点A关于x轴的对称点为P,求△PBC的面积.
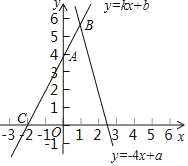
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣  x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π). -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x3﹣3x的图象如图所示,则以下关于该函数图象及其性质的描述正确的是( )
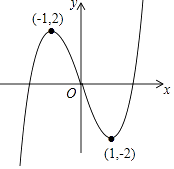
A.函数最大值为2
B.函数图象最低点为(1,﹣2)
C.函数图象关于原点对称
D.函数图象关于y轴对称
相关试题

