【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
参考答案:
【答案】
(1)解:已知:抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9;
x﹣9;
当x=0时,y=﹣9,则:C(0,﹣9);
当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣9=0,得:x1=﹣3,x2=6,则:A(﹣3,0)、B(6,0);
x﹣9=0,得:x1=﹣3,x2=6,则:A(﹣3,0)、B(6,0);
∴AB=9,OC=9
(2)解:∵ED∥BC,
∴△AED∽△ABC,
∴ ![]() =(
=( ![]() )2,即:
)2,即: ![]() =(
=( ![]() )2,得:s=
)2,得:s= ![]() m2(0<m<9)
m2(0<m<9)
(3)解:解法一:∵S△ACE= ![]() AEOC=
AEOC= ![]() m×9=
m×9= ![]() m,
m,
∴S△CDE=S△ACE﹣S△ADE= ![]() m﹣
m﹣ ![]() m2=﹣
m2=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() .
.
∵0<m<9,
∴当m= ![]() 时,S△CDE取得最大值,最大值为
时,S△CDE取得最大值,最大值为 ![]() .此时,BE=AB﹣AE=9﹣
.此时,BE=AB﹣AE=9﹣ ![]() =
= ![]() .
.
记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC= ![]() =
= ![]() =3
=3 ![]() .
.
∵∠OBC=∠MBE,∠COB=∠EMB=90°.
∴△BO∽△BME,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴r= ![]() =
= ![]() .
.
∴所求⊙E的面积为:π( ![]() )2=
)2= ![]() π.
π.
解法二:∵S△AEC= ![]() AEOC=
AEOC= ![]() m×9=
m×9= ![]() m,
m,
∴S△CDE=S△AEC﹣S△ADE= ![]() m﹣
m﹣ ![]() m2=﹣
m2=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() .
.
∵0<m<9,
∴当m= ![]() 时,S△CDE取得最大值,最大值为
时,S△CDE取得最大值,最大值为 ![]() .此时,BE=AB﹣AE=9﹣
.此时,BE=AB﹣AE=9﹣ ![]() =
= ![]() .
.
∴S△EBC= ![]() S△ABC=
S△ABC= ![]() .
.
如图2,记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC= ![]() =
= ![]() .
.
∵S△EBC= ![]() BCEM,∴
BCEM,∴ ![]() ×
× ![]() r=
r= ![]() ,
,
∴r= ![]() =
= ![]() .
.
∴所求⊙E的面积为:π( ![]() )2=
)2= ![]() π.
π.
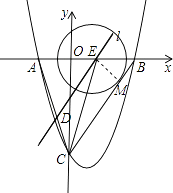
【解析】(1)已知抛物线的解析式,当x=0,可确定C点坐标;当y=0时,可确定A、B点的坐标,进而确定AB、OC的长.(2)直线l∥BC,可得出△AED、△ABC相似,它们的面积比等于相似比的平方,由此得到关于s、m的函数关系式;根据题干条件:点E与点A、B不重合,可确定m的取值范围.(3)①首先用m列出△AEC的面积表达式,△AEC、△AED的面积差即为△CDE的面积,由此可得关于S△CDE、m的函数关系式,根据函数的性质可得到S△CDE的最大面积以及此时m的值;②过E做BC的垂线EM,这个垂线段的长即为与BC相切的⊙E的半径,可根据相似三角形△BEF、△BCO得到的相关比例线段求得该半径的值,由此得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC,BD相交于点O,OB=OD,BD=CD,∠BAC=∠BDC=90°.
(1)填空:∠ABD=∠ ;
(2)求
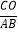 的值;
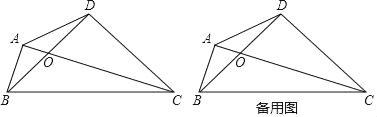
的值;(3)点D关于直线BC的对称点为N,连接AN,请补全图形,探究线段AN,AD有怎样的关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B
(1)求直线l的表达式;
(2)若点B的横坐标是1,求关于x、y的方程组
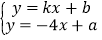 的解及a的值.
的解及a的值.(3)若点A关于x轴的对称点为P,求△PBC的面积.
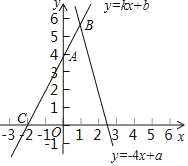
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x3﹣3x的图象如图所示,则以下关于该函数图象及其性质的描述正确的是( )
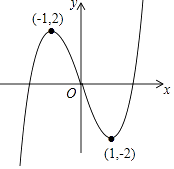
A.函数最大值为2
B.函数图象最低点为(1,﹣2)
C.函数图象关于原点对称
D.函数图象关于y轴对称 -
科目: 来源: 题型:
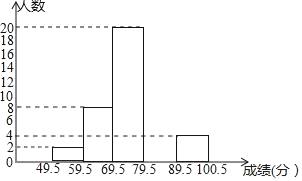
查看答案和解析>>【题目】某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末考试数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是 ;
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有
 ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.分组
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100.5
合计
频数
2
8
20
a
4
c
频率
0.04
b
0.40
0.32
0.08
1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有个点
 ,点
,点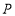 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点 ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点 ,第3次向上跳动1个单位到达
,第3次向上跳动1个单位到达 ,第4次向右跳动3个单位到达
,第4次向右跳动3个单位到达 ,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点
,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点 的坐标为( ).
的坐标为( ).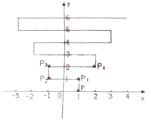
A.
 B.
B. C.
C. D.
D.
相关试题

