搜索
【题目】画图,并完成填空：
已知直角三角形ABC,∠C=90°
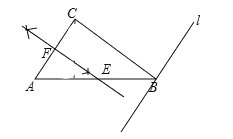
(1)过点B作直线1平行于AC
(2)利用尺规,画出线段AC的垂直平分线EF,交AB于点E,AC于点F
(3)点A到点E的距离是线段 的长,点A到BC的距离是线段 的长，直线L与AC的距离是线段 的长
参考答案：
【答案】（1）见解析；（2）见解析；（3）AE，AC，BC．
【解析】
（1）根据平行线的定义作图即可；
（2）根据尺规作线段垂直平分线的方法作图即可；
（3）根据两点之间的距离、点到直线的距离和平行线间的距离的定义，解答即可.
解：（1）直线l如图所示；；
（2）线段AC的垂直平分线EF如图所示；
（3）点A到点E的距离是线段AE的长，点A到BC的距离是线段AC的长，直线l与AC的距离是线段BC的长．
故答案为：AE，AC，BC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首．今年某校为确保学生安全，开展了“远离溺水珍爱生命”的防溺水安全知识竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A．80≤x＜85，B．85≤x＜90，C．90≤x＜95，D．95≤x≤100），下面给出了部分信息：七年级10名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82；八年级10名学生的竞赛成绩在C组中的数据是：94，90，94.
七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
根据以上信息，解答下列问题：
（1）直接写出上述图表中a，b，c的值；
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）；
（3）该校七、八年级共720人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≥90）的学生人数是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，直线y=
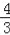x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．（1）求抛物线F1所表示的二次函数的表达式；
（2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；
（3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】图1是长方形纸带,将纸带沿折叠成图2,再沿即折叠成图3,若在图1中∠DEF=a，则图3中∠CFE用含有a的式子表示=_______(0<a<60°) .
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列四个函数：
①y=kx（k为常数，k＞0）
②y=kx+b（k，b为常数，k＞0）
③y=
（k为常数，k＞0，x＞0）④y=ax2（a为常数，a＞0）
其中，函数y的值随着x值得增大而减少的是（ ）
A. ① B. ② C. ③ D. ④
-
科目： 来源： 题型：
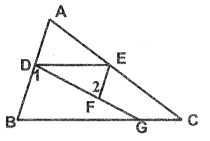
查看答案和解析>>【题目】已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ （ ）
所以∠B+∠BDE=180°（ ）
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180°（ ）
所以 ∥ （ ）
所以∠1=∠2（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
在进行二次根式的化简与运算时，我们有时会碰上如
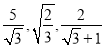样的式子，其实我们还可以将其进一步化简：（1）
···(一)（2）
···(二)（3）
···(三)以上这种化简的步骤叫做分母有理化．
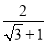还可以用以下方法化简：
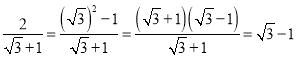···(四)请完成下列问题：
（1）请计算
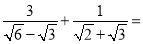；（2）当
，则代数式
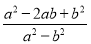的值为 ；（3）请参照(三)式和(四)式用两种不同的方法化简
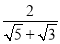
（4）化简：
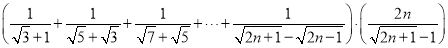
相关试题
