【题目】数学课上,张老师举了以下的例题:
例1等腰三角形ABC中,![]() ,求
,求![]() 的度数.(答案:35°)
的度数.(答案:35°)
例2等腰三角形ABC中,![]() ,求
,求![]() 的度数.(答案:40°或70°或100°)
的度数.(答案:40°或70°或100°)
张老师启发同学们编题,小刚编了如下一题:
(1)等腰三角形ABC中,![]() ,则
,则![]() 的度数为______;(2)小刚发现,
的度数为______;(2)小刚发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形ABC中,设
的度数的个数也可能不同.如果在等腰三角形ABC中,设![]() ,当
,当![]() 有三个不同的度数时,x的取值范围是______.
有三个不同的度数时,x的取值范围是______.
参考答案:
【答案】50°或20°或80°; ![]() 且
且![]() .
.
【解析】
(1)根据文中举出的例子分三种情况:①∠A为顶角时;②∠A为底角,∠B为顶角时;③∠A为底角,∠B为底角,据此分类讨论即可;
(2)分两种情况:①![]() ,②
,②![]() ,结合三角形内角和定理进一步求解即可.
,结合三角形内角和定理进一步求解即可.
(1):①∠A为顶角时,∠B=(180°-80°)÷2=50°;
②∠A为底角,∠B为顶角时,∠B=180°-2×80°=20°;
③∠A为底角,∠B为底角,∠B=∠A=80°;
故答案为:50°或20°或80°;
(2)①当![]() 时,∠A只能为顶角,∴此时∠B度数只有一个;
时,∠A只能为顶角,∴此时∠B度数只有一个;
②当![]() 时,
时,
若∠A为顶角,则∠B=(180°-x°)÷2;
若∠A为底角,∠B为顶角,则∠B=180°-2x°;
若∠A为底角,∠B为底角,则∠B=∠A=x°,
当(180°-x°)÷2≠180°-2x°,且180°-2x°≠x°且(180°-x°)÷2≠x°,
即![]() 时,∠B有三个不同的度数;
时,∠B有三个不同的度数;
综上所述,当![]() 且
且![]() 时,∠B有三个不同的度数.
时,∠B有三个不同的度数.
故答案为:![]() 且
且![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-12a2b2c)·(-
 abc2)2;
abc2)2;(2)(3a2b-4ab2-5ab-1)·(-2ab2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有三个分别写有数字6,﹣2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于10的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

-
科目: 来源: 题型:
查看答案和解析>>【题目】天津市奥林匹克中心体育场—“水滴”位于天津市西南部的奥林匹克中心内,某校九年级学生由距“水滴”10千米的学校出发前往参观,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.
(1)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)
速度(千米/时)
所用时间(时)
所走的路程(千米)
骑自行车
x
10
乘汽车
10
(2)列出方程(组),并求出问题的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
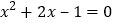 ,则此方程( )
,则此方程( )A. 无实数根 B. 两根之和为
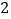 C. 两根之积为
C. 两根之积为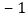 D. 有一个根为
D. 有一个根为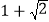
-
科目: 来源: 题型:
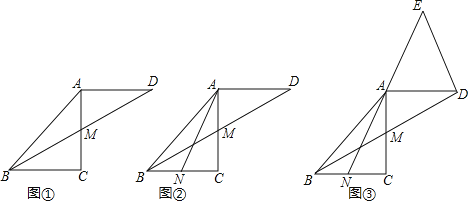
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
相关试题

