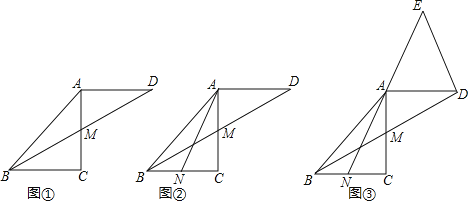
【题目】已知△ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
参考答案:
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)利用SAS进行证明即可;
(2)由点M是AC的中点,点N是BC的中点,AC=BC,可得CM=CN,继而利用SAS进行证明即可;
②取AD中点F,连接EF,则AD=2AF,由△BCM≌△ACN,△DAM≌△BCM,可推导得出AF=CN,∠EAF=∠ANC,根据SAS可证明△EAF≌△ANC,从而可得∠NAC=∠AEF,∠C=∠AFE=90°,进而可得∠AFE=∠DFE=90°,继而可以证明△AFE≌△DFE,则有∠EAD=∠EDA=∠ANC,继而可得∠EDB=90°,问题得证.
(1)∵点M是AC的中点,∴AM=CM,
在△DAM和△BCM中,
∵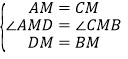 ,∴△DAM≌△BCM(SAS);
,∴△DAM≌△BCM(SAS);
(2)①∵点M是AC的中点,点N是BC的中点,∴CM=![]() AC,CN=
AC,CN=![]() BC,
BC,
∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,
在△BCM和△ACN中,∵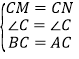 ,∴△BCM≌△ACN(SAS);
,∴△BCM≌△ACN(SAS);
②取AD中点F,连接EF,

则AD=2AF,
∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,
∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,
∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC,
∴AD∥BC,∴∠EAF=∠ANC.
在△EAF和△ANC中,∵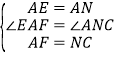 ,∴△EAF≌△ANC(SAS),
,∴△EAF≌△ANC(SAS),
∴∠NAC=∠AEF,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,
∵F为AD的中点,∴AF=DF,
在△AFE和△DFE中,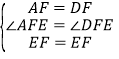 ,
,
∴△AFE≌△DFE(SAS),
∴∠EAD=∠EDA=∠ANC,
∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°–∠DAM=180°–90°=90°,
∴BD⊥DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了以下的例题:
例1等腰三角形ABC中,
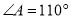 ,求
,求 的度数.(答案:35°)
的度数.(答案:35°)例2等腰三角形ABC中,
 ,求
,求 的度数.(答案:40°或70°或100°)
的度数.(答案:40°或70°或100°)张老师启发同学们编题,小刚编了如下一题:
(1)等腰三角形ABC中,
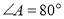 ,则
,则 的度数为______;(2)小刚发现,
的度数为______;(2)小刚发现,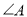 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形ABC中,设
的度数的个数也可能不同.如果在等腰三角形ABC中,设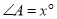 ,当
,当 有三个不同的度数时,x的取值范围是______.
有三个不同的度数时,x的取值范围是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】天津市奥林匹克中心体育场—“水滴”位于天津市西南部的奥林匹克中心内,某校九年级学生由距“水滴”10千米的学校出发前往参观,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.
(1)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)
速度(千米/时)
所用时间(时)
所走的路程(千米)
骑自行车
x
10
乘汽车
10
(2)列出方程(组),并求出问题的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
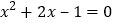 ,则此方程( )
,则此方程( )A. 无实数根 B. 两根之和为
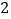 C. 两根之积为
C. 两根之积为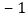 D. 有一个根为
D. 有一个根为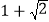
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图等腰
 ,
, ,
, ,
, 于点D,点P是BA延长线上一点,点O是线段AD上一点,
于点D,点P是BA延长线上一点,点O是线段AD上一点, ,下面的结论:
,下面的结论: ;
; 是等边三角形;
是等边三角形; ;
; 其中正确的是
其中正确的是


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽均为
 的纸条,交叉叠放在一起,且它们的交角为
的纸条,交叉叠放在一起,且它们的交角为 ,则它们重叠部分的面积为( )
,则它们重叠部分的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

