【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

参考答案:
【答案】(1)y=6.4x+32;(2)当购买数量x=35时,W总费用最低,W最低=137元.
【解析】
试题(1)利用得到系数法求解析式,列出方程组解答即可;(2)根据所需费用为W=A种树苗的费用+B种树苗的费用,即可解答.
试题解析:(1)设y与x的函数关系式为:y=kx+b, 把(20,160),(40,288)代入y=kx+b得:
![]() 解得:
解得:![]() ∴y=6.4x+32.
∴y=6.4x+32.
(2)∵B种苗的数量不超过35棵,但不少于A种苗的数量,∴![]() ∴22.5≤x≤35,
∴22.5≤x≤35,
设总费用为W元,则W=6.4x+32+7(45﹣x)=﹣0.6x+347,
∵k=﹣0.6, ∴y随x的增大而减小, ∴当x=35时,W总费用最低,W最低=﹣0.6×35+347=137(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从圆形跑道(圆形跑道的总长小于700m)上一直径两端A,B相向起跑.第一次相遇时离A点100m,第二次相遇时离B点60m,则圆形跑道的总长为( )
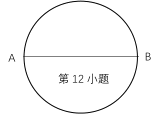
A.240mB.360mC.480mD.600m
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-12a2b2c)·(-
 abc2)2;
abc2)2;(2)(3a2b-4ab2-5ab-1)·(-2ab2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有三个分别写有数字6,﹣2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于10的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了以下的例题:
例1等腰三角形ABC中,
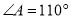 ,求
,求 的度数.(答案:35°)
的度数.(答案:35°)例2等腰三角形ABC中,
 ,求
,求 的度数.(答案:40°或70°或100°)
的度数.(答案:40°或70°或100°)张老师启发同学们编题,小刚编了如下一题:
(1)等腰三角形ABC中,
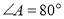 ,则
,则 的度数为______;(2)小刚发现,
的度数为______;(2)小刚发现,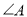 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形ABC中,设
的度数的个数也可能不同.如果在等腰三角形ABC中,设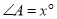 ,当
,当 有三个不同的度数时,x的取值范围是______.
有三个不同的度数时,x的取值范围是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】天津市奥林匹克中心体育场—“水滴”位于天津市西南部的奥林匹克中心内,某校九年级学生由距“水滴”10千米的学校出发前往参观,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.
(1)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)
速度(千米/时)
所用时间(时)
所走的路程(千米)
骑自行车
x
10
乘汽车
10
(2)列出方程(组),并求出问题的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
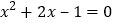 ,则此方程( )
,则此方程( )A. 无实数根 B. 两根之和为
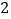 C. 两根之积为
C. 两根之积为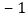 D. 有一个根为
D. 有一个根为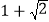
相关试题

