【题目】如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线DB于点F,AF交⊙O于点H,连结BH.
(1)求证:AC=CD;
(2)若OB=2,求BH的长.

参考答案:
【答案】(1)证明见解析;(2)BH的长为![]()
【解析】试题分析:(1)连接OC,只要证明OC∥BD即可.
(2)在Rt△ABF中,根据BH=![]() 计算即可.
计算即可.
试题解析:证明(1)连接OC.
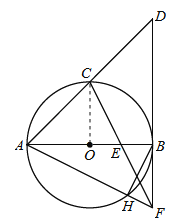
∵C是弧AB中点,AB是○O的直径,∴OC⊥AB.∵BD是○O切线,∴BD⊥AB,∴OC∥BD.∵AO=BO,∴AC=CD;
(2)∵E是OB中点,∴OE=BE.在△COE与△FBE中,∵∠CEO=∠FEB,OE=BE,∠COE=∠FBE,∴△COE≌△FBE(ASA),∴BF=CO.
∵OB=2,∴BF=2,∴AF=![]() =
=![]() =
=![]() .
.
∵AB是直径,∴BH⊥AF,∴ABBF=AFBH,∴BH=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
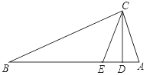
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+8(k<0)交y轴于点A,交x轴于点B.将△AOB关于直线AB翻折得到△APB.过点A作AC∥x轴交线段BP于点C,在AC上取点D,且点D在点C的右侧,连结BD.
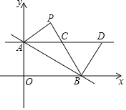
(1)求证:AC=BC
(2)若AC=10.
①求直线AB的表达式.
②若△BCD是以BC为腰的等腰三角形,求AD的长.
(3)若BD平分∠OBP的外角,记△APC面积为S1,△BCD面积为S2,且
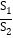 =
= ,则
,则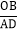 的值为______(直接写出答案)
的值为______(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
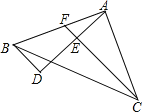
A. 6B. 5C. 4D. 8
-
科目: 来源: 题型:
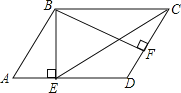
查看答案和解析>>【题目】在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求
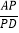 的值.
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:
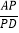 的值为 .
的值为 .参考小昊思考问题的方法,解决问题:
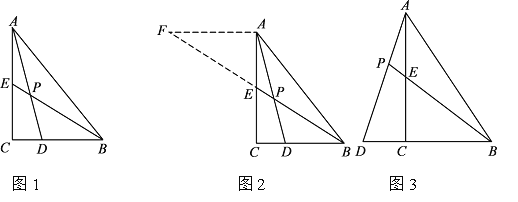
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求
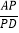 的值;
的值;(2)若CD=2,则BP=__________.
相关试题

