【题目】阅读下面材料:
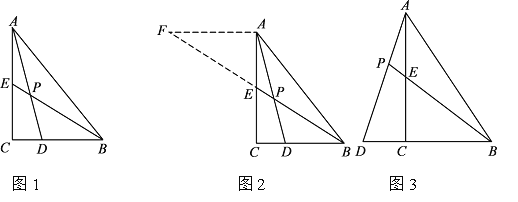
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
参考答案:
【答案】![]() 的值为
的值为![]() ;(1)
;(1)![]() ;(2) 6.
;(2) 6.
【解析】试题分析:易证△AEF≌△CEB,则有AF=BC.设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,然后根据相似三角形的性质就可求出![]() 的值;
的值;
解决问题:(1)过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出![]() 的值;
的值;
(2)当CD=2时,可依次求出BC、AC、EC、EB、EF、BF的值,然后根据![]() 的值求出
的值求出![]() ,就可求出BP的值.
,就可求出BP的值.
试题解析:解:![]() 的值为
的值为![]() .
.
易证△AEF≌△CEB,则有AF=BC.
设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,即可得到![]() =
=![]() =
=![]() .故答案为:
.故答案为:![]() ;
;
解决问题:
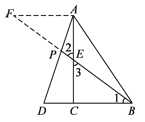
(1)过点A作AF∥DB,交BE的延长线于点F,如图,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.∵E是AC中点,∴AE=CE.∵AF∥DB,∴∠F=∠1.
在△AEF和△CEB中,∵∠F=∠1,∠2=∠3,AE=CE,∴△AEF≌△CEB,∴EF=BE,AF=BC=2k.∵AF∥DB,∴△AFP∽△DBP,∴![]() =
=![]() ,∴
,∴![]() 的值为
的值为![]() ;
;
(2)当CD=2时,BC=4,AC=6,∴EC=![]() AC=3,EB=
AC=3,EB=![]() =5,∴EF=BE=5,BF=10.∵
=5,∴EF=BE=5,BF=10.∵![]() (已证),∴
(已证),∴![]() ,∴BP=
,∴BP=![]() BF=
BF=![]() ×10=6.
×10=6.
故答案为:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线DB于点F,AF交⊙O于点H,连结BH.
(1)求证:AC=CD;
(2)若OB=2,求BH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
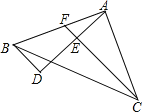
A. 6B. 5C. 4D. 8
-
科目: 来源: 题型:
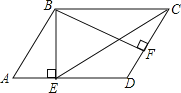
查看答案和解析>>【题目】在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,点D从点B出发,沿B→C方向运动到点C(D不与B,C重合),连接AD,作∠ADE=30°,DE交线段AC于点E.设∠B4D=x°,∠AED=y°.
(1)当BD=AD时,求∠DAE的度数;
(2)求y与x的关系式;
(3)当BD=CE时,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, P 是直线 l 外一点,点 A、B、C 在 l 上,且 PB l ,下列说法:① PA、PB、PC 这 3 条线段中, PB 最短;②点 P 到直线 l 的距离是线段 PB 的长;③线段 AB 的长是点 A 到 PB 的距离;④线段 PA 的长是点 P 到直线 l 的距离. 其中正确的是( )
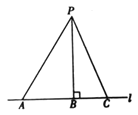
A. ①②③B. ①②④C. ①③④D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AB=10,BD=8,∠ACD=45°.
(1)求线段AD的长;
(2)求△ABC的周长.

相关试题

