【题目】如图,直线y=kx+8(k<0)交y轴于点A,交x轴于点B.将△AOB关于直线AB翻折得到△APB.过点A作AC∥x轴交线段BP于点C,在AC上取点D,且点D在点C的右侧,连结BD.
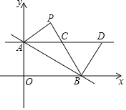
(1)求证:AC=BC
(2)若AC=10.
①求直线AB的表达式.
②若△BCD是以BC为腰的等腰三角形,求AD的长.
(3)若BD平分∠OBP的外角,记△APC面积为S1,△BCD面积为S2,且![]() =
=![]() ,则
,则![]() 的值为______(直接写出答案)
的值为______(直接写出答案)
参考答案:
【答案】(1)证明见解析;(2)①y=-![]() x+8;②20或22;(3)
x+8;②20或22;(3)![]() .
.
【解析】
(1)由平行线的性质可得出∠BAC=∠ABO,由折叠的性质可知∠ABO=∠ABC,进而可得出∠BAC=∠ABC,由等角对等边即可证出AC=BC;
(2)过点B作BE⊥CD于点E.①利用一次函数图象上点的坐标特征可求出OA的长度,进而可得出BE的长度,在Rt△BCE中,利用勾股定理可求出CE的长度,进而可得出OB,AE的长度,由OB的长度可得出点B的坐标,再利用待定系数法即可求出直线AB的表达式;
②分BC=DC及BC=BD两种情况考虑:当BC=DC时,由AC=BC=10,可求出AD的长度;当BC=BD时,利用等腰三角形的性质结合①的结论可求出CD的长度,进而可得出AD的长度.综上,此问得解;
(3)由折叠的性质结合三角形的面积公式可得出![]() ,设PC=2a,则CD=3a,易证△APC≌△BEC(AAS),由全等三角形的性质可得出CE=CP=2a,由角平分线的定义、平行线的性质结合等腰三角形的性质可得出CB=CD=AC=3a,在Rt△BCE中,CE=2a,进而可得出OB=5a,AD=6a,二者相比后即可得出
,设PC=2a,则CD=3a,易证△APC≌△BEC(AAS),由全等三角形的性质可得出CE=CP=2a,由角平分线的定义、平行线的性质结合等腰三角形的性质可得出CB=CD=AC=3a,在Rt△BCE中,CE=2a,进而可得出OB=5a,AD=6a,二者相比后即可得出![]() 的值.
的值.
(1)证明:∵AC∥x轴,
∴∠BAC=∠ABO.
由折叠的性质,可知:∠ABO=∠ABC,
∴∠BAC=∠ABC,
∴AC=BC.
(2)解:过点B作BE⊥CD于点E,如图1所示.
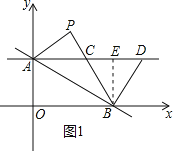
①当x=0时,y=kx+8=8,
∴点A的坐标为(0,8),BE=OA=8.
在Rt△BCE中,BC=AC=10,BE=8,
∴CE=![]() =6,
=6,
∴OB=AE=AC+CE=16,
∴点B的坐标为(16,0).
将点B(16,0)代入y=kx+8,得:0=16k+8,
解得:k=-![]() ,
,
∴直线AB的表达式为y=-![]() x+8.
x+8.
②当BC=DC时,AD=AC+CD=10+10=20;
当BC=BD时,由①可知:CD=2CE=12,
∴AD=AC+CD=10+12=22.
综上:AD的长为20或22.
(3)由折叠的性质,可知:AO=AP,∠APC=∠AOB=90°.
∵S△APC=![]() APPC=
APPC=![]() AOPC,S△BCD=
AOPC,S△BCD=![]() CDAO,OA=BE,
CDAO,OA=BE,
∴![]() =
=![]() ,
,
设PC=2a,则CD=3a.
在△APC和△BEC中,
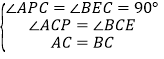 ,
,
∴△APC≌△BEC(AAS),
∴PC=EC.
∵BD平分∠OBP的外角,CD∥x轴,
∴∠CBD=∠CDB,
∴CD=CB=3a.
在Rt△BCE中,CB=3a,CE=2a,
∴BE=![]() =
=![]() a,
a,
∴OB=AC+CE=CD+CE=5a,AD=AC+CD=2CD=6a,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于依次排列的多项式x+a,x+b,x+c,x+d(a,b,c,d是常数),当它们满足在
 ,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为
,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为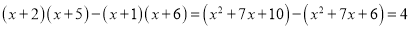 ,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.
,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.(1)已知2,4,7,9是一组平衡数,求该组平衡数的平衡因子M;
(2)若a,b,c,d是一组平衡数,a=-4,d=3,请直接写出组b,c的值;
(3)当a,b,c,d之间满是什么数量关系时,它们是一组平衡数,并说明理由.
-
科目: 来源: 题型:
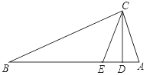
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线DB于点F,AF交⊙O于点H,连结BH.
(1)求证:AC=CD;
(2)若OB=2,求BH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
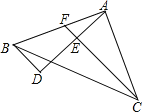
A. 6B. 5C. 4D. 8
-
科目: 来源: 题型:
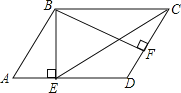
查看答案和解析>>【题目】在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为_____________.
相关试题

