【题目】已知二次函数中x和y的部分对应值如下表:
x … ﹣1 0 1 2 3 …
y … 0 ﹣3 ﹣4 ﹣3 0 …
(1)求二次函数的解析式;
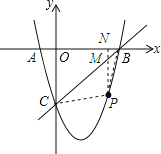
(2)如图,点P是直线BC下方抛物线上一动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积;

(3)在抛物线上,是否存在一点Q,使△QBC中QC=QB?若存在请直接写出Q点的坐标.
参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)P(![]() ,﹣
,﹣![]() ),
),![]() ;(3)Q1(
;(3)Q1(![]() ,﹣
,﹣![]() )、Q2(
)、Q2(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)利用待定系数法即可求得二次函数的解析式;
(2)首先求得直线BC的解析式,过P作PN⊥x轴交直线BC于点M,然后根据S△BPC=S△PCM+S△PMB=![]() PMON+
PMON+![]() PMNB,即可把S△BPC表示成P的横坐标x的函数,根据函数的性质求最值;
PMNB,即可把S△BPC表示成P的横坐标x的函数,根据函数的性质求最值;
(3)QC=QB,则Q就是线段BC的中垂线与二次函数的交点,首先求得BC的解析式,然后解方程组即可.
解:(1)设y=a(x+1)(x﹣3)把(0,﹣3)代入可得:﹣3=a(0+1)(0﹣3)
解得:a=1则y=(x+1)(x﹣3)=x2﹣2x﹣3,
∴二次函数的解析式为:y=x2﹣2x﹣3;
(2)S四边形ABPC=S△ABC+S△BPC=![]() ×1×3+S△BPC,
×1×3+S△BPC,
设直线BC的解析式是y=kx+b,
则![]() ,
,
解得:![]() ,
,
则直线BC的解析式是:y=x﹣3.
过P作PN⊥x轴交直线BC于点M,设P(x,x2﹣2x﹣3)则M(x,x﹣3)
∴MP=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x
S△BPC=S△PCM+S△PMB=![]() PMON+
PMON+![]() PMNB
PMNB
=![]() PMOB=
PMOB=![]() (﹣x2+3x)×3=﹣
(﹣x2+3x)×3=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() (0<x<3).
(0<x<3).
当x=![]() 时,S△BPC的最大值为
时,S△BPC的最大值为![]() ,则 S四边形ABPC的最大值为:
,则 S四边形ABPC的最大值为:![]() +
+![]() =
=![]() ,
,
此时P(![]() ,﹣
,﹣![]() );
);
(3)BC的中点坐标是(![]() ,﹣
,﹣![]() ).
).
设线段BC的中垂线的解析式是y=﹣x+c,则﹣![]() +c=﹣
+c=﹣![]() ,
,
解得c=0,
即BC的中垂线的解析式是y=﹣x.
根据题意得:![]() ,
,
解得: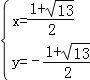 或
或 .
.
则Q的坐标是:Q1(![]() ,﹣
,﹣![]() )、Q2(
)、Q2(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边等于4,一边等于7,那么它的周长等于 ( )
A.12 B.18 C.12或21 D.15或18
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,∠DBA=60°,把△ABD绕点B逆时针旋转使得点A落在BD上,点A对称点为点A1,点D对称点为点D1,A1 D1与BC交于点E,连接D1C.

(1)求证:EC=EA1;
(2)求证:点D1、C、D在同一直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
阅读下列材料:
1×2=
 (1×2×3﹣0×1×2),
(1×2×3﹣0×1×2),2×3=
 (2×3×4﹣1×2×3),
(2×3×4﹣1×2×3),3×4=
 (3×4×5﹣2×3×4),
(3×4×5﹣2×3×4),由以上三个等式相加,可得1×2+2×3+3×4=
 ×3×4×5=20
×3×4×5=20读完以上材料,请你计算下列各题,其中(1)需要写出过程,其它试题直接写出答案.
(1)1×2+2×3+3×4+…+6×7= ;
(2)1×2+2×3+3×4+…+n×(n+1)= ;
(3)1×2+2×3+3×4+3×4×5+…+6×7×8= ;
(4)1×2+2×3+3×4+3×4×5+…+n×(n+1)×(n+2)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)﹣
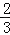 ﹣
﹣ ﹣(﹣
﹣(﹣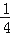 )﹣
)﹣
(2)9.872+(﹣
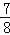 )+(﹣5.872)
)+(﹣5.872)(3)(
 ﹣
﹣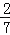
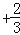 )÷(﹣
)÷(﹣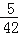 );
);(4)
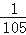
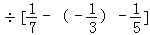
(5)1.3×(﹣9.12)+(﹣7)×9.12
(6)﹣14﹣
 ×[2﹣(﹣3)]2
×[2﹣(﹣3)]2(7)[
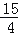 ÷(﹣
÷(﹣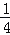 )+0.4×
)+0.4×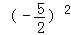 ]×(﹣1)5
]×(﹣1)5(8)[1
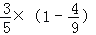 ]2÷[(1﹣
]2÷[(1﹣ )×
)×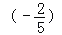 ]3.
]3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,直径AB⊥弦CD于点E,四边形ADCF是平行四边形,CD=4
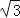 ,BE=2.
,BE=2.
(1)求⊙O直径和弦AD的长;
(2)求证:FC是⊙O切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3×9m×27m=321,求m的值.
相关试题

