搜索
【题目】在直角坐标系中，点A、B的坐标分别为（﹣2，4）、（﹣5，2），点M、N分别是x轴、y轴上的点，若以点A、B、M、N为顶点的四边形是平行四边形，则点M的横坐标的所有可能的值是 ．
参考答案：
【答案】﹣7，﹣3，3
【解析】解：如图所示：
当AB平行且等于N1M1时，四边形ABM1N1是平行四边形；
当AB平行且等于N2M2时，四边形ABN2M2是平行四边形；
当AB为对角线时，四边形AN3BM3是平行四边形．
故符合题意的有3个点，点M的横坐标分别为﹣7，﹣3，3．
所以答案是：﹣7，﹣3，3．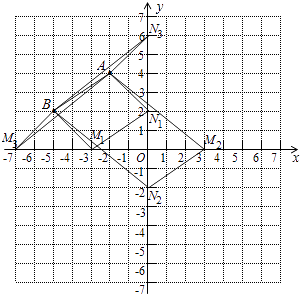
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．
-
科目： 来源： 题型：
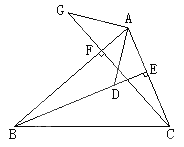
查看答案和解析>>【题目】（10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）问题：如图（1），在Rt△ACB中，∠ACB=90°，AC=CB，∠DCE=45°，试探究AD、DE、EB满足的等量关系．
[探究发现]
小聪同学利用图形变换，将△CAD绕点C逆时针旋转90°得到△CBH，连接EH，由已知条件易得∠EBH=90°，∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°．根据“边角边”，可证△CEH≌ ，得EH=ED．
在Rt△HBE中，由 定理，可得BH2+EB2=EH2，由BH=AD，可得AD、DE、EB之间的等量关系是 ．
[实践运用]
（1）如图（2），在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等，求∠EAF的度数；
（2）在（1）条件下，连接BD，分别交AE、AF于点M、N，若BE=2，DF=3，BM=2
，运用小聪同学探究的结论，求正方形的边长及MN的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A. 2x2x3=2x6 B. （﹣2a）3=﹣6a3 C. （a3）2=a5 D. x3÷x2=x
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程
（1）
=
（2）
+
= 
（3）先化简，再求值（
﹣ 
）÷ 
，其中a=1，b=2． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴建立平面直角坐标系，点B的坐标为（2，0），扇形的圆心角是60°，若抛物线 y=x+k与扇形OAB的边界总有两个公共点，则实数取值范围是
A. -4＜k＜
B. -2＜k＜
C. -4＜k＜
D. --2＜k＜
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A（体操）、B（乒乓球）、C（毽球）、D（跳绳）四项活动．为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：
（1）这次被调查的学生共有人；
（2）请将统计图2补充完整；
（3）统计图1中B项目对应的扇形的圆心角是度；
（4）已知该校共有学生1000人，根据调查结果估计该校喜欢体操的学生有人．
相关试题
