【题目】（10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD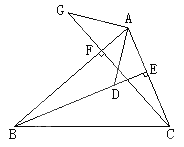

参考答案：

【答案】可证明△EBM≌△FCM，

得∠EMB≌△FCM，

得∠EMB＝∠FMC，

∵∠CMF＋∠BMF＝180°

∴∠BME＋∠BMF＝180°

∴E、F、M恰好在一直线上

【解析】分析：三角形全等条件中必须是三个元素，本题已经有两条对应边相等，只要再找到它们的夹角相等就可以了．

解答：证明：∵BE、CF分别是AC、AB两条边上的高，

∴∠ABD+∠BAC=90°，

∠GCA+∠BAC=90°，

∴∠GCA=∠ABD，

在△GCA和△ABD中，

，

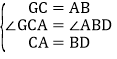∴△GCA≌△ABD．

∴AG=AD．

关闭