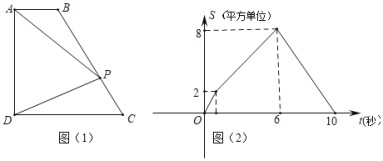
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
A. 4B. 5C. 6D. 7
参考答案:
【答案】B
【解析】
根据函数图象和三角形面积得出AB+BC=6,CD=4,AD=4,AB=1,当P运动到BC中点时,梯形ABCD的中位线也是△APD的高,求出梯形ABCD的中位线长,再代入三角形面积公式即可得出结果.
解:根据题意得:四边形ABCD是梯形,AB+BC=6,CD=10-6=4,
∵![]() AD×CD=8,
AD×CD=8,
∴AD=4,
又∵![]() AD×AB=2,
AD×AB=2,
∴AB=1,
当P运动到BC中点时,梯形ABCD的中位线也是△APD的高,
∵梯形ABCD的中位线长=![]() (AB+CD)=
(AB+CD)=![]() ,
,
∴△PAD的面积![]()
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=﹣
 x2﹣
x2﹣ x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.(1)求这条抛物线的解析式;
(2)如图2,D点在x轴上,且在A点的右侧,E点为抛物线上第二象限内的点,连接ED交抛物线于第二象限内的另外一点F,点E到y轴的距离与点F到y轴的距离之比为3:1,已知tan∠BDE=
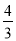 ,求点E的坐标;
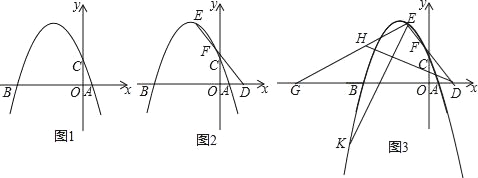
,求点E的坐标;(3)如图3,在(2)的条件下,点G由B出发,沿x轴负方向运动,连接EG,点H在线段EG上,连接DH,∠EDH=∠EGB,过点E作EK⊥DH,与抛物线相应点E,若EK=EG,求点K的坐标.
-
科目: 来源: 题型:
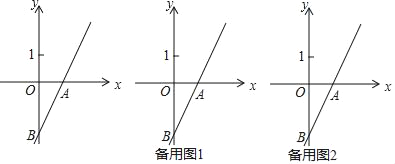
查看答案和解析>>【题目】如图,直线y=2x﹣2与x轴交于点A,与y轴交于点B.点C是该直线上不同于B的点,且CA=AB.
(1)写出A、B两点坐标;
(2)过动点P(m,0)且垂直于x轴的直线与直线AB交于点D,若点D不在线段BC上,求m的取值范围;
(3)若直线BE与直线AB所夹锐角为45°,请直接写出直线BE的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从边长为
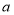 的正方形内去掉一个边长为
的正方形内去掉一个边长为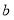 的小正方形,然后将剩余部分拼成一个长方形。
的小正方形,然后将剩余部分拼成一个长方形。(1)上述操作所能验证的公式是 ;
(2)求大正方形和拼成的长方形的周长;
(3)用一根长为
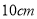 的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?
的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?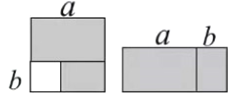
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
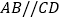 ,
,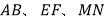 相交于
相交于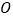 点,
点,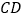 与
与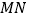 相交于点
相交于点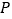 ,
,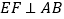 ,
,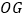 为
为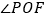 的平分线,
的平分线,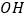 为
为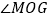 的平分线。
的平分线。(1)若
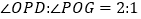 ,求
,求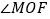 的大小;
的大小;(2)若
 ,求
,求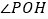 的大小。
的大小。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

-
科目: 来源: 题型:
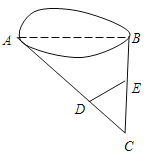
查看答案和解析>>【题目】如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离。
相关试题

