【题目】如图,直线y=2x﹣2与x轴交于点A,与y轴交于点B.点C是该直线上不同于B的点,且CA=AB.
(1)写出A、B两点坐标;
(2)过动点P(m,0)且垂直于x轴的直线与直线AB交于点D,若点D不在线段BC上,求m的取值范围;
(3)若直线BE与直线AB所夹锐角为45°,请直接写出直线BE的函数解析式.
参考答案:
【答案】(1)A(1,0),B(0,﹣2);(2)m<0或m>2;(3)y=![]() x﹣2或y=﹣3x﹣2.
x﹣2或y=﹣3x﹣2.
【解析】
(1)利用待定系数法即可解决问题;
(2)如图1中,作CF⊥x轴与F.利用全等三角形的性质求出点F坐标即可判断;
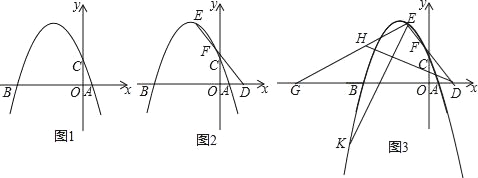
(3)如图2中,作AE⊥AB,使得AE=AB,作EH⊥x轴于H,则△ABE是等腰直角三角形,∠ABE=45°.利用全等三角形的性质求出点E坐标,当直线BE′⊥直线BE时,直线BE′也满足条件,求出直线BE′的解析式即可;
解:(1)对于直线y=2x﹣2令x=0,得到y=﹣2,令y=0,得到x=1,
∴A(1,0),B(0,﹣2).
(2)如图1中,作CF⊥x轴与F.
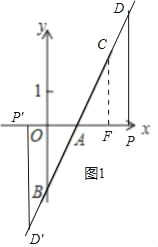
∵CA=AB,∠CAF=∠OAB,∠CFA=∠AOB=90°,
∴△CAF≌△BAO,
∴AF=OA=1,CF=OB=2,
∴F(2,0),
观察图象可知m的取值范围为:m<0或m>2.
(3)如图2中,作AE⊥AB,使得AE=AB,作EH⊥x轴于H,则△ABE是等腰直角三角形,∠ABE=45°.
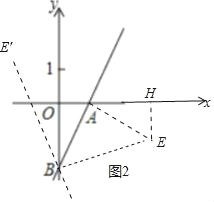
∵∠AOB=∠BAE=∠AHE=90°,
∴∠OAB+∠ABO=90°,∠OAB+∠HAE=90°,
∴∠ABO=∠HAE,∵AB=AE,
∴△ABO≌△EAH,
∴AH=OB=2,EH=OA=1,
∴E(3,﹣1),
设直线BE的解析式为y=kx+b,则有![]()
解得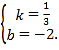
∴直线BE的解析式为![]() ,
,
当直线BE′⊥直线BE时,直线BE′也满足条件,直线BE′的解析式为y=﹣3x﹣2,
∴满足条件的直线BE的解析式为![]() 或y=﹣3x﹣2.
或y=﹣3x﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副直角三角尺如图①叠放,先将含
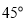 角的三角尺
角的三角尺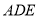 固定不动,含角
固定不动,含角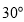 的三角尺
的三角尺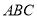 绕顶点
绕顶点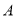 顺时针旋转
顺时针旋转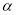 (
(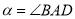 且
且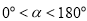 ),使两块三角尺至少有一组边平行.
),使两块三角尺至少有一组边平行.
完成下列任务:(温馨提示:先用你的三角尺拜摆一摆)
(1)填空:如图②,当
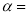 时
时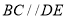 ,;
,;(2)请你分别在图③、图④中各画出一种符合要求的图形,标出
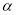 ,并完成下列问题:
,并完成下列问题:图③中,当
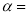 时,
时,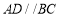 ;
;图④中,当
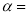 时,
时,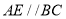 或者
或者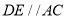 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y=
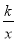 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+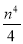 .
.(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠
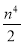 ,求OP2的最小值.
,求OP2的最小值.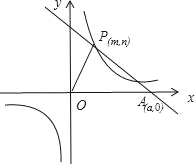
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=﹣
 x2﹣
x2﹣ x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.(1)求这条抛物线的解析式;
(2)如图2,D点在x轴上,且在A点的右侧,E点为抛物线上第二象限内的点,连接ED交抛物线于第二象限内的另外一点F,点E到y轴的距离与点F到y轴的距离之比为3:1,已知tan∠BDE=
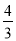 ,求点E的坐标;
,求点E的坐标;(3)如图3,在(2)的条件下,点G由B出发,沿x轴负方向运动,连接EG,点H在线段EG上,连接DH,∠EDH=∠EGB,过点E作EK⊥DH,与抛物线相应点E,若EK=EG,求点K的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从边长为
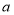 的正方形内去掉一个边长为
的正方形内去掉一个边长为 的小正方形,然后将剩余部分拼成一个长方形。
的小正方形,然后将剩余部分拼成一个长方形。(1)上述操作所能验证的公式是 ;
(2)求大正方形和拼成的长方形的周长;
(3)用一根长为
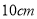 的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?
的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?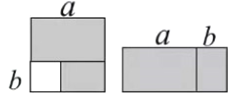
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
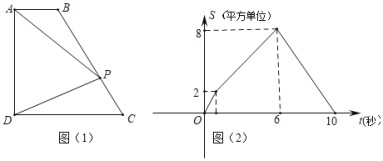
A. 4B. 5C. 6D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
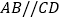 ,
,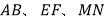 相交于
相交于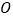 点,
点, 与
与 相交于点
相交于点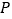 ,
,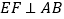 ,
,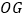 为
为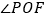 的平分线,
的平分线,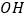 为
为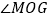 的平分线。
的平分线。(1)若
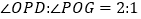 ,求
,求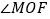 的大小;
的大小;(2)若
 ,求
,求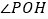 的大小。
的大小。
相关试题

