【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足![]() .
.
(1)写出a、b及AB的距离:a=________;b=________;AB=________.
(2)若动点P从点A出发,以每秒3个点位长度沿数轴向右匀速运动,动点Q从点B出发,以每秒5个单位长度向右匀速运动,若P、Q同时出发,问点Q运动多少秒追上点P?
![]()
![]()
参考答案:
【答案】(1)a=8,b=5,AB=13;(2)点Q运动![]() 秒时追上点P.
秒时追上点P.
【解析】
(1)利用绝对值的非负性即可求得a、b,进而求得AB的长;
(2)根据题意,设点Q运动t秒时追上点P,则Q运动路程为5t,P运动路程为3t,利用追及问题公式,列出方程,即可解答.
(1)因为![]() .
.
所以a-8=0,b+5=0
所以a=8,b=5,AB=13
(2)设点Q运动t秒时追上点P,则Q运动路程为5t,P运动路程为3t
则5t3t=13,
∴t=![]() ,即:点Q运动
,即:点Q运动![]() 秒时追上点P.
秒时追上点P.
-
科目: 来源: 题型:
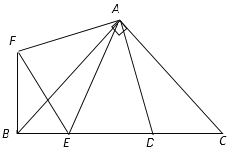
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
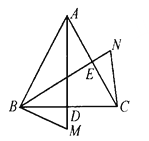
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点表示的数分别为-4,8.有一动点P从点A出发,第1次向左运动1个单位长度,第2次向右运动2个单位长度,第3次向左运动3个单位长度……按照此规律不断地运动.
(1)①当运动到第2020次时,点P表示的数是_______;
②点A与点B的距离AB=_______;
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若存在,请求出此时点P表示的数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
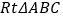 中,
中,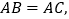
 是斜边
是斜边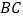 上两点,且
上两点,且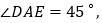 将
将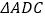 绕点
绕点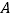 顺时针旋转90°后,得到
顺时针旋转90°后,得到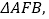 连接
连接
(1)求证: △AED≌△AEF
(2)猜想线段BE,ED,DC之间的关系,并证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=
 时, 若CD=
时, 若CD= ,求AD长.
,求AD长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求
 的值.
的值.(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则
 =
= 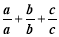 =1+1+1=3;
=1+1+1=3;②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则
 =
= 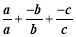 =111=1;
=111=1;所以
 的值为3或1.
的值为3或1. (探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求
 的值;
的值;(2)已知
 =9,
=9,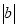 =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
相关试题

