【题目】已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.

参考答案:
【答案】(1)△DEF是等腰直角三角形,理由详见解析;(2)EF=2![]() cm.
cm.
【解析】
(1)连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)延长ED至G,使得DG=DE,连接FG,CG,判定△BDE≌△CDG,即可得出CG=BE=2cm,∠B=∠DCG=45°=∠ACB,利用勾股定理可得,Rt△CFG中,FG=![]() =2
=2![]() cm,再根据FD垂直平分EG,即可得到EF=GF=2
cm,再根据FD垂直平分EG,即可得到EF=GF=2![]() cm.
cm.
解:(1)△DEF是等腰直角三角形.
如图,连接AD,

∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=![]() BC=BD=CD,且AD平分∠BAC,
BC=BD=CD,且AD平分∠BAC,
∴∠BAD=∠CAD=45°,
在△BDE和△ADF中,
 ,
,
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,即∠EDF=90°,
∴△EDF为等腰直角三角形.
(2)如图,延长ED至G,使得DG=DE,连接FG,CG,
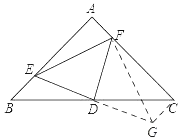
∵D为BC的中点,
∴BD=CD,
又∵∠BDE=∠CDG,
∴△BDE≌△CDG,
∴CG=BE=2cm,∠B=∠DCG=45°=∠ACB,
∴∠GCF=90°,
又∵CF=4cm,
∴Rt△CFG中,FG=![]() =
=![]() =2
=2![]() cm,
cm,
∵∠EDF=90°,ED=GD,
∴FD垂直平分EG,
∴EF=GF=2![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:
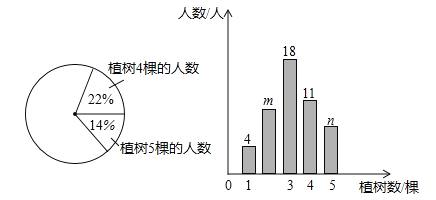
(1)八年级三班共有多少名同学?
(2)条形统计图中,m= ,n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
-
科目: 来源: 题型:
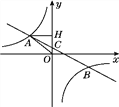
查看答案和解析>>【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
-
科目: 来源: 题型:
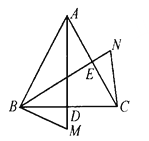
查看答案和解析>>【题目】如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点表示的数分别为-4,8.有一动点P从点A出发,第1次向左运动1个单位长度,第2次向右运动2个单位长度,第3次向左运动3个单位长度……按照此规律不断地运动.
(1)①当运动到第2020次时,点P表示的数是_______;
②点A与点B的距离AB=_______;
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若存在,请求出此时点P表示的数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足
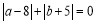 .
.(1)写出a、b及AB的距离:a=________;b=________;AB=________.
(2)若动点P从点A出发,以每秒3个点位长度沿数轴向右匀速运动,动点Q从点B出发,以每秒5个单位长度向右匀速运动,若P、Q同时出发,问点Q运动多少秒追上点P?


相关试题

