【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求![]() 的值.
的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则![]() =
= ![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则![]() =
= ![]() =111=1;
=111=1;
所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(2)已知![]() =9,
=9,![]() =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
参考答案:
【答案】(1)-3或1;(2)17或1.
【解析】
(1)按照题目内的求值方式,分类讨论,即可解答.
(2)根据![]() =9,
=9,![]() =4分别求出a、b的值,再根据a<b,分情况讨论,分别求出a2b的值即可.
=4分别求出a、b的值,再根据a<b,分情况讨论,分别求出a2b的值即可.
(1)∵abc<0,
∴a,b,c都是负数或其中一个为负数,另两个为正数,
①当a,b,c都是负数,即a<0,b<0,c<0时,则原式=111=3;
②a,b,c有一个为负数,另两个为正数时,不妨设a<0,b>0,c>0,则原式=1+1+1=1;
(2) ∵ ![]() =9,
=9,![]() =4
=4
∴a=![]() 9,b=±4
9,b=±4
∵a<b,
∴当a=-9,b=4时,a2b=92×4=-17,
当a=-9,b=-4时,a2b=92×(-4)=-1,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足
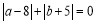 .
.(1)写出a、b及AB的距离:a=________;b=________;AB=________.
(2)若动点P从点A出发,以每秒3个点位长度沿数轴向右匀速运动,动点Q从点B出发,以每秒5个单位长度向右匀速运动,若P、Q同时出发,问点Q运动多少秒追上点P?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
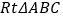 中,
中,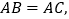
 是斜边
是斜边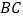 上两点,且
上两点,且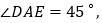 将
将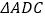 绕点
绕点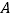 顺时针旋转90°后,得到
顺时针旋转90°后,得到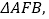 连接
连接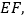
(1)求证: △AED≌△AEF
(2)猜想线段BE,ED,DC之间的关系,并证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=
 时, 若CD=
时, 若CD= ,求AD长.
,求AD长.
-
科目: 来源: 题型:
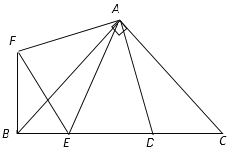
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,并写出点C2的坐标;
(3)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
-
科目: 来源: 题型:
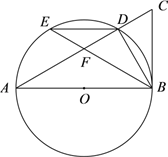
查看答案和解析>>【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在网上销售苹果,原计划每天卖100斤,但实际每天的销量与计划销量相比有出入,如表是某周7天的销售情况(超额记为正,不足记为负.单位:斤):

(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 斤;
(2)本周实际销售总量达到了计划销量没有?
(3)若每斤按5元出售,每斤苹果的运费为1元,那么小明本周一共收入多少元?
相关试题

