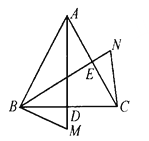
【题目】如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
参考答案:
【答案】见解析
【解析】
根据等边三角形的性质可得∠ABC=∠ACB=60°,AB=BC,然后求出∠ABM=∠BCN,再根据等边三角形三线合一的性质求出∠BAM=∠CBN=30°,然后利用“角边角”证明△ABM和△BCN全等,再根据全等三角形对应边相等证明即可.
:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵∠CBM=∠ACN,
∴∠ABC+∠CBM=∠ACB+∠ACN,
即∠ABM=∠BCN,
∵AD、BE分别是边BC、AC上的高,
∴∠BAM=∠CBN=30°,
在△ABM和△BCN中,
∠ABM=∠BCN AB=BC ∠BAM=∠CBN,
∴△ABM≌△BCN(ASA),
∴AM=BN.
-
科目: 来源: 题型:
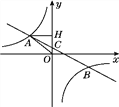
查看答案和解析>>【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点表示的数分别为-4,8.有一动点P从点A出发,第1次向左运动1个单位长度,第2次向右运动2个单位长度,第3次向左运动3个单位长度……按照此规律不断地运动.
(1)①当运动到第2020次时,点P表示的数是_______;
②点A与点B的距离AB=_______;
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若存在,请求出此时点P表示的数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足
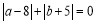 .
.(1)写出a、b及AB的距离:a=________;b=________;AB=________.
(2)若动点P从点A出发,以每秒3个点位长度沿数轴向右匀速运动,动点Q从点B出发,以每秒5个单位长度向右匀速运动,若P、Q同时出发,问点Q运动多少秒追上点P?


-
科目: 来源: 题型:
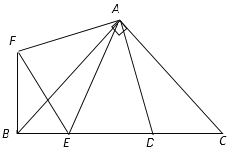
查看答案和解析>>【题目】如图,在
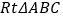 中,
中,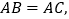
 是斜边
是斜边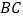 上两点,且
上两点,且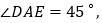 将
将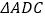 绕点
绕点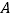 顺时针旋转90°后,得到
顺时针旋转90°后,得到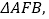 连接
连接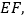
(1)求证: △AED≌△AEF
(2)猜想线段BE,ED,DC之间的关系,并证明
相关试题

