【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每月可卖出
元,每月可卖出![]() 件.市场调查反映:调整价格时,售价每涨
件.市场调查反映:调整价格时,售价每涨![]() 元每月要少卖
元每月要少卖![]() 件;售价每下降
件;售价每下降![]() 元每月要多卖
元每月要多卖![]() 件.为了获得更大的利润,现将饰品售价调整为
件.为了获得更大的利润,现将饰品售价调整为![]() (元/件)(
(元/件)(![]() 即售价上涨,
即售价上涨,![]() 即售价下降),每月饰品销量为
即售价下降),每月饰品销量为![]() (件),月利润为
(件),月利润为![]() (元).
(元).
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如何确定销售价格才能使月利润最大?求最大月利润;
如何确定销售价格才能使月利润最大?求最大月利润;
![]() 为了使每月利润不少于
为了使每月利润不少于![]() 元应如何控制销售价格?
元应如何控制销售价格?
参考答案:
【答案】(1)![]() (2)当销售价格为
(2)当销售价格为![]() 元时,利润最大,最大利润为
元时,利润最大,最大利润为![]() 元(3)将销售价格控制在
元(3)将销售价格控制在![]() 元到
元到![]() 元之间(含
元之间(含![]() 元和
元和![]() 元)才能使每月利润不少于
元)才能使每月利润不少于![]() 元
元
【解析】
(1)直接根据题意售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件,进而得出等量关系;
(2)利用每件利润×销量=总利润,进而利用配方法求出即可;
(3)利用函数图象结合一元二次方程的解法得出符合题意的答案.
解:![]() 由题意可得:
由题意可得:![]() ;
;![]() 由题意可得:
由题意可得:![]() ,
,
化简得:![]() ,
,
即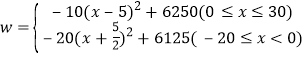 ,
,
由题意可知![]() 应取整数,故当
应取整数,故当![]() 或
或![]() 时,
时,![]() ,
,
故当销售价格为![]() 元时,利润最大,最大利润为
元时,利润最大,最大利润为![]() 元;
元;![]() 由题意
由题意![]() ,如图,令
,如图,令![]() ,
,
即![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
故将销售价格控制在![]() 元到
元到![]() 元之间(含
元之间(含![]() 元和
元和![]() 元)才能使每月利润不少于
元)才能使每月利润不少于![]() 元.
元.
-
科目: 来源: 题型:
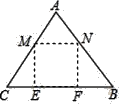
查看答案和解析>>【题目】如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
-
科目: 来源: 题型:
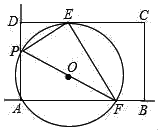
查看答案和解析>>【题目】如图,矩形ABCD中,AD=10,CD=15,E是边CD上一点,且DE=5,P是射线AD上一动点,过A,P,E三点的⊙O交直线AB于点F,连结PE,EF,PF,设AP=m.
(1)当m=6时,求AF的长.
(2)在点P的整个运动过程中.
①tan∠PFE的值是否改变?若不变,求出它的值;若改变,求出它的变化范围.
②当矩形ABCD恰好有2个顶点落在⊙O上时,求m的值.
(3)若点A,H关于点O成中心对称,连结EH,CH.当△CEH是等腰三角形时,求出所有符合条件的m的值.(直接写出答案即可)
-
科目: 来源: 题型:
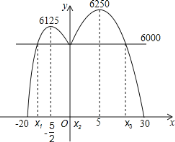
查看答案和解析>>【题目】二次函数
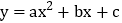 的图象如图所示,下列结论错误的是( )
的图象如图所示,下列结论错误的是( )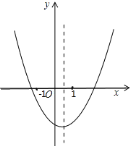
A. b2-4ac>0 B. a-b+c<0 C. abc<0 D. 2a+b>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】饮水机接通电源就进入自动程序,若在水温为
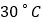 时,接通电源后,水温
时,接通电源后,水温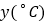 和时间
和时间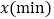 的关系如图.开机加热时每分钟上升
的关系如图.开机加热时每分钟上升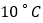 ,加热到
,加热到 ,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至
,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至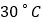 ,饮水机自动开机,重复上述自动程序.若上午
,饮水机自动开机,重复上述自动程序.若上午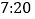 开机,则
开机,则 时能否喝到超过
时能否喝到超过 的水?说明理由.
的水?说明理由.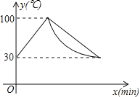
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为 1 的正方形组成的网格中,△ ABC的顶点均在格点上,A(3,2), B(4, 3), C(1, 1)

(1)画出△ABC关于y轴对称的图形△ A′B′C′
(2)写出A′、B′、C′的坐标(直接写出答案) A′ ;B′ ;C′ ;
(3)写出△ A′B′C′的面积为 .(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置,图 2 是由它抽像出的几何图形,B, C, E在同一 条直线上,连结DC.

(1)请找出图 2 中的全等三角形,并给予证明(说明:结论中不得含有未标识的字 母);
(2)证明:DC ⊥ BE.
相关试题

