【题目】如图,在边长为 1 的正方形组成的网格中,△ ABC的顶点均在格点上,A(3,2), B(4, 3), C(1, 1)

(1)画出△ABC关于y轴对称的图形△ A′B′C′
(2)写出A′、B′、C′的坐标(直接写出答案) A′ ;B′ ;C′ ;
(3)写出△ A′B′C′的面积为 .(直接写出答案)
参考答案:
【答案】(1)见解析;(2)(3,2),(4,-3),(1,-1),(3)![]()
【解析】
(1)根据关于y轴对称的点的坐标特点即可得知A′,B′,C′的坐标,描出这些点依次连接即可得出△ A′B′C′;
(2)根据(1)所画图形即可得各点坐标;
(3)用割补法即可求出△ A′B′C′的面积.
(1)因为A(3,2), B(4, 3), C(1, 1) ,关于y轴对称,所以A′(3,2),B′(4,-3),C′(1,-1),依次描出三点,连接即可,见下图:

(2)根据(1)作图过程可知A′(3,2),B′(4,-3),C′(1,-1)
(3)![]() ,过程如下:
,过程如下:
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
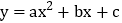 的图象如图所示,下列结论错误的是( )
的图象如图所示,下列结论错误的是( )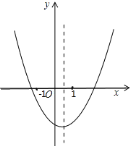
A. b2-4ac>0 B. a-b+c<0 C. abc<0 D. 2a+b>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件
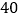 元,售价为每件
元,售价为每件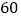 元,每月可卖出
元,每月可卖出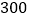 件.市场调查反映:调整价格时,售价每涨
件.市场调查反映:调整价格时,售价每涨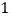 元每月要少卖
元每月要少卖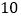 件;售价每下降
件;售价每下降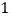 元每月要多卖
元每月要多卖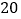 件.为了获得更大的利润,现将饰品售价调整为
件.为了获得更大的利润,现将饰品售价调整为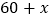 (元/件)(
(元/件)( 即售价上涨,
即售价上涨, 即售价下降),每月饰品销量为
即售价下降),每月饰品销量为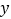 (件),月利润为
(件),月利润为 (元).
(元).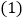 直接写出
直接写出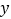 与
与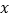 之间的函数关系式;
之间的函数关系式;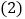 如何确定销售价格才能使月利润最大?求最大月利润;
如何确定销售价格才能使月利润最大?求最大月利润;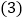 为了使每月利润不少于
为了使每月利润不少于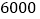 元应如何控制销售价格?
元应如何控制销售价格? -
科目: 来源: 题型:
查看答案和解析>>【题目】饮水机接通电源就进入自动程序,若在水温为
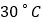 时,接通电源后,水温
时,接通电源后,水温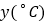 和时间
和时间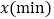 的关系如图.开机加热时每分钟上升
的关系如图.开机加热时每分钟上升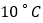 ,加热到
,加热到 ,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至
,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至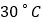 ,饮水机自动开机,重复上述自动程序.若上午
,饮水机自动开机,重复上述自动程序.若上午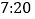 开机,则
开机,则 时能否喝到超过
时能否喝到超过 的水?说明理由.
的水?说明理由.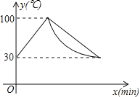
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置,图 2 是由它抽像出的几何图形,B, C, E在同一 条直线上,连结DC.

(1)请找出图 2 中的全等三角形,并给予证明(说明:结论中不得含有未标识的字 母);
(2)证明:DC ⊥ BE.
-
科目: 来源: 题型:
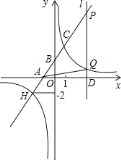
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线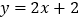 与
与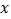 轴、
轴、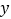 轴分别交于点
轴分别交于点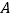 、
、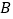 ,与双曲线
,与双曲线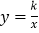 交于第一象限的点
交于第一象限的点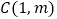 和第三象限的点
和第三象限的点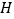 ,
, 点的纵坐标为
点的纵坐标为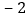
 求
求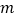 和
和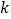 的值;
的值; 求不等式:
求不等式: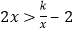 的解集
的解集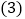 过
过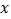 轴上的点
轴上的点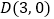 作平行于
作平行于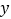 轴的直线
轴的直线 ,分别与直线
,分别与直线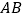 和双曲线
和双曲线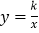 交于点
交于点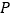 、
、 ,求
,求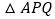 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】 (1)阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ= QR = RS,(这个条件很重要哦!)勾 尺的一边 MN 满足M, N, Q三点共线(所以PQ ⊥ MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE //BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP:
请完成第三步操作,图中∠ABC的三等分线是射线 、 .
(2)在(1)的条件下补全三等分∠ABC的主要证明过程:
∵ ,BQ ⊥ PR,
∴BP= BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)
∴∠RBQ=∠PBQ,
∵PT⊥BC,PQ⊥BQ,PT=PQ,
∴∠ = ∠ . (角的内部到角的两边距离相等的点在角的平分线上)
∴∠ = = ∠ = ∠
(3)在(1)的条件下探究:
∠ABS=
 ∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC外部画出∠ABV =
∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC外部画出∠ABV = ∠ABC(无需写画法,保留画图痕迹即可)
∠ABC(无需写画法,保留画图痕迹即可) 
相关试题

