【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).

参考答案:
【答案】树高为9米.
【解析】
试题分析:过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
试题解析:如图,过点A作AF⊥DE于F,
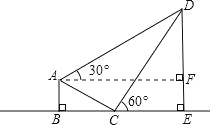
则四边形ABEF为矩形,
∴AF=BE,EF=AB=3米,
设DE=x,
在Rt△CDE中,CE=![]() x,
x,
在Rt△ABC中,
∵![]() ,AB=3,
,AB=3,
∴BC=3![]() ,
,
在Rt△AFD中,DF=DE-EF=x-3,
∴AF=![]() (x-3),
(x-3),
∵AF=BE=BC+CE,
∴![]() (x-3)=3
(x-3)=3![]() +
+![]() x,
x,
解得x=9(米).
答:树高为9米.
-
科目: 来源: 题型:
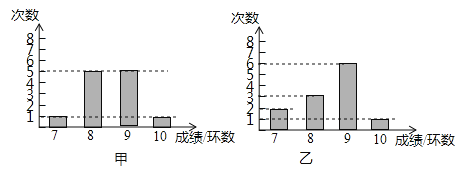
查看答案和解析>>【题目】甲乙两人进行射击训练,两人分别射击12次,如图分别统计了两人的射击成绩,已知甲射击成绩的方差
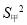 =
=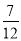 ,平均成绩
,平均成绩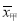 =8.5.
=8.5.(1)根据图上信息,估计乙射击成绩不少于9环的概率是多少?
(2)求乙射击的平均成绩的方差,并据此比较甲乙的射击“水平”.
S2=
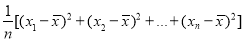 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(4×104)×(2×103)﹣(6.5×103)×(6×103)
(2)(a﹣1)2+(a+3)(a﹣3)+(a﹣3)(a﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子从左到右的变形中,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1
B.x2﹣2x+1=x(x﹣2)+1
C.a2﹣b2=(a+b)(a﹣b)
D.(m﹣n)m=m2﹣mn -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题是( )
A.等腰三角形两腰上的高相等
B.面积相等的两个三角形全等
C.两条直线被第三条直线所截,内错角相等
D.一个角的两边与另一个角的两边分别平行,那么这两个角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长为( )
A. 3cm B. 4 cm C. 5cm D. 6 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】几何图形根据是否在同一平面内分为___________图形和_________图形.
相关试题

