【题目】如图,△ABC为等边三角形,AB=8,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边作等边△CEF,连接DF,则线段DF的最小值为( )

A.![]() B.4C.2D.无法确定
B.4C.2D.无法确定
参考答案:
【答案】C
【解析】
连接BF,由等边三角形的性质可得三角形全等的条件,从而可证△BCF≌△ACE,推出∠CBF=∠CAE=30°,再由垂线段最短可知当DF⊥BF时,DF值最小,利用含30°的直角三角形的性质定理可求DF的值.
如图,连接BF,
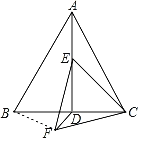
∵△ABC为等边三角形,AD⊥BC,AB=8,
∴BC=AC=AB=8,BD=DC=4,∠BAC=∠ACB=60°,∠CAE=30°,
∵△CEF为等边三角形,
∴CF=CE,∠FCE=60°,
∴∠FCE=∠ACB,
∴∠BCF=∠ACE,
∴在△BCF和△ACE中,
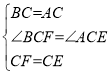 ,
,
∴△BCF≌△ACE(SAS),
∴∠CBF=∠CAE=30°,AE=BF,
∴当DF⊥BF时,DF值最小,
此时∠BFD=90°,∠CBF=30°,BD=4,
∴DF=2,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

(1)根据上表填空:
①抛物线与x轴的交点坐标是______和______;
②抛物线经过点(-3,______);
(2)试确定抛物线y=ax2+bx+c的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北 方向为 x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表 100m 长.已知 各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).

(1)请写出图中下列地点的坐标:
牡丹园 ; 游乐园 ;
(2)连接音乐台、湖心亭和望春亭这三个 地点,画出所得的三角形.然后将所 得三角形向下平移 200m,画出平移后的图形;
(3)问题(2)中湖心亭平移后的对应点的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=
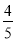 ,求BF的长.
,求BF的长.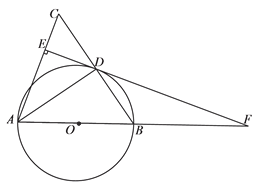
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出A、B两种园艺造型共50个,搭造要求的花盆数如下表所示:
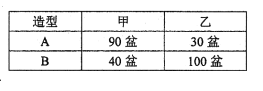
请问符合要求的搭造方案有几种?请写出具体的方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可 得六边形 ABCDEF 中必有两条边是平行的.

(1)根据图形写出你的猜想: ∥ ;
(2)请证明你在(1)中写出的猜想.
相关试题

