【题目】如图,AB是⊙O的直径,CO⊥AB于点O,CD是⊙O的切线,切点为D.连接BD,交OC于点E. 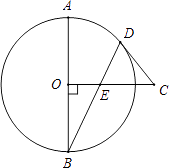
(1)求证:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的长.
参考答案:
【答案】
(1)证明:连接OD,
∵CD是⊙O的切线,切点为D.
∴∠ODC=90°,
∵OD=OB,∴∠B=∠ODB,
∵OC⊥AB,
∴∠CED=∠OEB=90°﹣∠B,
∵∠CDE=90°﹣∠ODB,
∴∠CDE=∠CED;
(2)连接AD,

∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=13,
∴OB= ![]() ,
,
∵∠ADB=∠BOE,∠B=∠B,
∴△ABD∽△EBO,
∴ ![]() .
.
∴ ![]() ,
,
∴EB= ![]() ,
,
∴DE=BD﹣EB= ![]() .
.
【解析】(1)连接OD,利用切线的性质和圆的半径相等得到的等腰三角形即可证明∠CDE=∠CED;(2)连接AD,利用圆周角定理和已知条件证明△ABD∽△EBO,利用相似三角形的性质即可求出EB的长,进而求出DE的长.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A的坐标为(﹣2,﹣1),点B的坐标为(0,﹣2),若将线段AB平移至A′B′的位置,点A′的坐标为(a,2),点B′的坐标为(1,b),则a+b的值为( )
A. 0 B. 2 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某银行去年新增加居民存款10亿元人民币.
(1)经测量,100张面值为100元的新版人民币大约厚0.9厘米,如果将10亿元面值为100元的新版人民币摞起来,大约有多高?
(2)一台激光点钞机的点钞速度是8×104张/时,按每天点钞5小时计算,如果让点钞机点一遍10亿元面值为100元的新版人民币,点钞机大约要点多少天?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′,点B′恰好落在BC边土,B′C′和CD交于点P,则∠B′PD的度数是( )

A. 105° B. 120° C. 130° D. 135°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在周长为12的菱形ABCD中,CE=1,CF=2,若点P为对角线BD上一动点,则PE+PF的最小值是( )
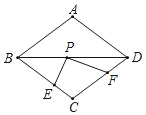
A.
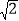 B. 2 C. 3 D. 5
B. 2 C. 3 D. 5
相关试题

