【题目】点A的坐标为(﹣2,﹣1),点B的坐标为(0,﹣2),若将线段AB平移至A′B′的位置,点A′的坐标为(a,2),点B′的坐标为(1,b),则a+b的值为( )
A. 0 B. 2 C. 4 D. 5
参考答案:
【答案】A
【解析】
利用A点坐标为 (-2, -1) , A′点坐标为 (a, 2)可得到线段AB向上平移3个单位至A′B′; 利用B点和B′点坐标得到线段AB向有平移1个单位至A′B′, 则根据线段平移的规律得到-2+1=a, -2+3=b,解得a=-1,b=1,然后计算a+b.
解:A(-2, -1), A′(a,2),
![]() 线段AB向上平移3个单位至A′B′;
线段AB向上平移3个单位至A′B′;
B(0,﹣2), B′(1,b), ![]() 线段 AB向右平移1个单位至AB;
线段 AB向右平移1个单位至AB;
即线段AB先向上平移3个单位,再向右平移1个单位得到A′B′,
-2+1=a, -2+3=b, 解得a=-1, b=1,
![]() a+b=-1+1=0.
a+b=-1+1=0.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示.
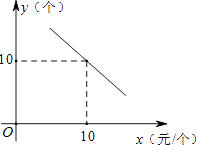
(1)求此一次函数的关系式;
(2)现批发市场进行促销活动,凭会员卡(240元/张)在该批发市场购买所有物品均进行打折优惠,若文具店购买A、B两种文具各50个,问打折小于多少折时,采用购买会员卡的方式合算;
(3)在文具店不购买会员卡的情况下,若A种文具零售价比B种文具零售价高2元/个,求这两种文具每天的销售总利润W(元)与A种文具零售价x(元/个)之间的函数关系式,并说明当A种文具的零售价为多少时,每天的销售利润最大. (说明:本题不要求写出自变量x的取值范围) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CO⊥AB于点O,CD是⊙O的切线,切点为D.连接BD,交OC于点E.
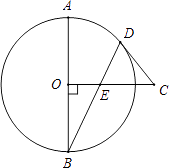
(1)求证:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某银行去年新增加居民存款10亿元人民币.
(1)经测量,100张面值为100元的新版人民币大约厚0.9厘米,如果将10亿元面值为100元的新版人民币摞起来,大约有多高?
(2)一台激光点钞机的点钞速度是8×104张/时,按每天点钞5小时计算,如果让点钞机点一遍10亿元面值为100元的新版人民币,点钞机大约要点多少天?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′,点B′恰好落在BC边土,B′C′和CD交于点P,则∠B′PD的度数是( )

A. 105° B. 120° C. 130° D. 135°
相关试题

