搜索
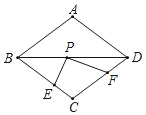
【题目】如图，在周长为12的菱形ABCD中，CE=1，CF=2，若点P为对角线BD上一动点，则PE+PF的最小值是（ ）
A. 
B. 2 C. 3 D. 5
参考答案：
【答案】C
【解析】
作F点关于BD的对称点F , 则PF=PF , 由两点之间线段最短可知当E、 P、 F 在一条直线上时,EP+FP有最小值, 然后求得EF 的长度即可.
解：如图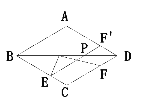
作F点关于BD的对称点F',则PF=PF',连接EF'交BD于点P.
EP+FP=EP+F'P.
由两点之间线段最短可知: 当E、P 、F'在一条直线上时,EP+FP的值最小,此时
EP+FP=EP+F'P=EF'.
四边形ABCD为菱形,周长为12,
AB=BC=CD=DA=3,AB //CD,
CF=2, CE=1,
D F'=DF=1,
四边形CEF'D是平行四边形,
EF'=CD=3.
EP+FP的最小值为3.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，CO⊥AB于点O，CD是⊙O的切线，切点为D．连接BD，交OC于点E．
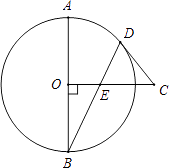
（1）求证：∠CDE=∠CED；
（2）若AB=13，BD=12，求DE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】某银行去年新增加居民存款10亿元人民币．
(1)经测量，100张面值为100元的新版人民币大约厚0.9厘米，如果将10亿元面值为100元的新版人民币摞起来，大约有多高？
(2)一台激光点钞机的点钞速度是8×104张/时，按每天点钞5小时计算，如果让点钞机点一遍10亿元面值为100元的新版人民币，点钞机大约要点多少天？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′，点B′恰好落在BC边土，B′C′和CD交于点P，则∠B′PD的度数是（ ）
A. 105° B. 120° C. 130° D. 135°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，点E、F分别是BC、CD上的点，且CE=CF，点P、Q分别是AF、EF的中点，连接PD、PQ、DQ，则△PQD的形状是（ ）
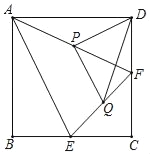
A. 等腰三角形 B. 直角三角形
C. 等腰非直角三角形 D. 等腰直角三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2+12x﹣30的顶点为A，对称轴AB与x轴交于点B．在x上方的抛物线上有C、D两点，它们关于AB对称，并且C点在对称轴的左侧，CB⊥DB．
（1）求出此抛物线的对称轴和顶点A的坐标；
（2）在抛物线的对称轴上找出点Q，使它到A、C两点的距离相等，并求出点Q的坐标；
（3）延长DB交抛物线于点E，在抛物线上是否存在点P，使得△DEP的面积等于△DEC的面积？若存在，请你直接写出点P的坐标；若不存在，请说明理由．
提示：抛物线y=ax2+bx+c（a≠0）的对称轴为
，顶点坐标为 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知正比例函数y=3x的图象与反比例函数y=
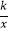的图象交于点A（1，m）和点B．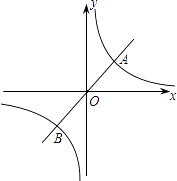 
（1）求m的值和反比例函数的解析式．
（2）观察图象，直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围．
相关试题
