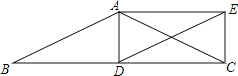
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析.
【解析】
试题分析:(1)、根据平行四边形的性质得出AB∥DE,AB=DE,∠B=∠EDC,根据AB=AC得出AC=DE,即∠EDC=∠ACD,从而得出三角形全等;(2)、根据ABDE为平行四边形得出BD∥AE,BD=AE,根据点D为中点得出BD=CD,AE=CD,从而说明四边形ADCE是平行四边形,根据AB=AC,BD=CD得出∠ADC=90°,从而得出四边形ADCE是矩形.
试题解析:(1)、∵四边形ABDE是平行四边形,∴AB∥DE,AB=DE,∴∠B=∠EDC 又∵AB=AC,∴AC=DE
∴∠EDC=∠ACD
在△ACD和△EDC中 ∴△ACD≌△EDC
∴△ACD≌△EDC
(2)、∵四边形ABDE是平行四边形,∴BD∥AE,BD=AE,∴AE∥CD
∵点D是BC中点,∴BD=CD,∴AE=CD,∴四边形ADCE是平行四边形
在△ABC中,AB=AC,BD=CD,∴AD⊥BC,∴∠ADC=90°,∴四边形ADCE是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
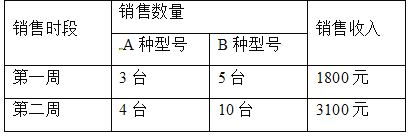
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
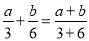 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: 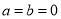 .我们称使得
.我们称使得 成立的一对数
成立的一对数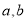 为“相伴数对”,记为(
为“相伴数对”,记为(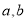 ).
).(1)若(
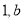 )是“相伴数对”,求b的值;
)是“相伴数对”,求b的值;(2)写出一个“相伴数对”(
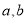 ),其中
),其中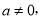 且
且 ;
;(3)若(
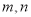 )是“相伴数对”,求代数式
)是“相伴数对”,求代数式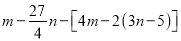 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读理解】对于任意正实数a、b,
∵(
 -
- )2≥0,∴a-2
)2≥0,∴a-2 +b≥0,
+b≥0,∴a+b≥2
 ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2 ).
).【获得结论】在a+b≥2
 (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,则a+b≥2
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
.根据上述内容,回答下列问题:(1)若
 >0,只有当
>0,只有当 = 时,m+
= 时,m+ 有最小值 .
有最小值 . 【探索应用】(2)已知点Q(-3,-4)是双曲线y=
 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y= (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5)
B.(3,﹣13)
C.(2,﹣8)
D.(4,﹣20) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是中心对称图形,又是轴对称图形的是( )
A.等边三角形
B.等腰三角形
C.平行四边形
D.线段
相关试题

