【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
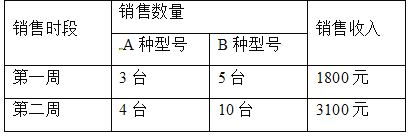
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)A、B两种型号电风扇的销售单价分别为250元、210元;(2)超市最多采购A种型号电风扇10台时,采购金额不多于5400元;(3)在(2)的条件下超市不能实现利润1400元的目标.
【解析】试题分析:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号5台B型号的电扇收入1800元,4台A型号10台B型号的电扇收入3100元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,根据金额不多余5400元,列不等式求解;
(3)设利润为1400元,列方程求出a的值为20,不符合(2)的条件,可知不能实现目标.
试题解析:(1)设A、B两种型号的电风扇的销售价分别为x、y元
则: ![]()
解得: ![]()
答:A、B两种型号电风扇的销售介分别为250元和210元。
②设采购A种型号电风扇a台,则采购B种型号的电风扇(30-a)台
则200a+170(30-a)≤540
解得a≤10
答:最多采购A种型号的电风扇10台。
③根据题意得(2500-200)a+(210-170)(30-a)=1400
解得a=20
∵a≤10
所以在(2)条件下超市销售完这30台电风扇不能实现利润为1400元的目标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3x2-2x+3的值是-4,则-9x2+6x-8的值是_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(x,3)与点B(2,y)关于x轴对称,则( )
A.x=﹣2,y=﹣3
B.x=2,y=3
C.x=﹣2,y=3
D.x=2,y=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】图象经过(1,2)的正比例函数的表达式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
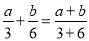 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: 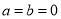 .我们称使得
.我们称使得 成立的一对数
成立的一对数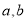 为“相伴数对”,记为(
为“相伴数对”,记为(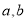 ).
).(1)若(
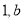 )是“相伴数对”,求b的值;
)是“相伴数对”,求b的值;(2)写出一个“相伴数对”(
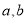 ),其中
),其中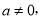 且
且 ;
;(3)若(
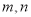 )是“相伴数对”,求代数式
)是“相伴数对”,求代数式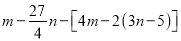 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
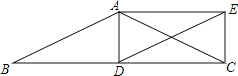
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
相关试题

