搜索
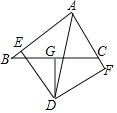
【题目】如图，△ABC中，BC=a，AC=b，AB=c（b＜c＜a），BC的垂直平分线DG交∠BAC的角平分线AD于点D，DE⊥AB于E，DF⊥AC于F，则下列结论一定成立的是（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】D
【解析】
如图，连接DB、DC．只要证明△DEB≌△DFC，推出BE=CF，由△ADE≌△ADF，推出AE=AF，推出AB+AC=（AE+BE）+（AF﹣CF）=2AE，即AE=
（AB+AC）．
如图，连接DB、DC．
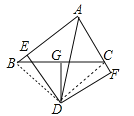
∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE=DF，∠DEB=∠DFC=90°．
∵DG垂直平分线段BC，∴DB=DC．
在Rt△DEB和Rt△DFC中，∵
，∴△DEB≌△DFC，∴BE=CF，同理△ADE≌△ADF，∴AE=AF，∴AB+AC=（AE+BE）+（AF﹣CF）=2AE，∴AE=（AB+AC）=（b+c）．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）．
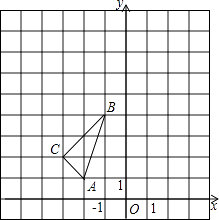
（1）①画出△ABC关于y轴对称的图形△A1B1C1 ， 并直接写出C1点坐标；
②以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A2B2C2 ， 并直接写出C2点坐标；
（2）如果点D（a，b）在线段AB上，请直接写出经过（1）②的变化后点D的对应点D2的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料．
点M，N在数轴上分别表示数m和n，我们把m，n之差的绝对值叫做点M，N之间的距离，即MN=|m﹣n|．如图，在数轴上，点A，B，O，C，D的位置如图所示，则DC=|3﹣1|=|2|=2；CO=|1﹣0|=|1|=1；BC=|（﹣2）﹣1|=|﹣3|=3；AB=|（﹣4）﹣（﹣2）|=|﹣2|=2．
（1）OA= ，BD= ；
（2）|1﹣（﹣4）|表示哪两点的距离？
（3）点P为数轴上一点，其表示的数为x，用含有x的式子表示BP= ，当BP=4时，x= ；当|x﹣3|+|x+2|的值最小时，x的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了合理利用电力资源，缓解用电紧张状况，我国电力部门出台了使用“峰谷电”的政策及收费标准(见下表)．
用电时间段
收费标准
峰电
08：00—22：00
0.56元/千瓦时
谷电
22：00—08：00
0.28元/千瓦时
已知王老师家4月份使用“峰谷电”95千瓦时，缴电费43.40元，问王老师家4月份“峰电”和“谷电”各用了多少千瓦时？设王老师家4月份“峰电”用了x千瓦时，“谷电”用了y千瓦时，根据题意，列方程组得_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C，D和E，B分别是∠MAN的边AM和AN上的两点，且AC=AB，AD=AE，CE和BD相交于F点，给出下列结论：①△ABD≌△ACE；②△BFE≌△CFD；③F在∠MAN的平分线上．其中正确的是______．
-
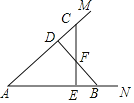
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，四边形ABCD中，∠A与∠B互补，∠C=90°，DE⊥AB，E为垂足．若∠EDC=60°，求∠B、∠A及∠ADE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F．
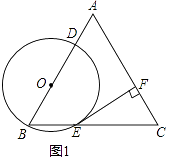
（1）求证：直线EF是⊙O的切线；
（2）如图2，当直线AC与⊙O相切时，求⊙O的半径．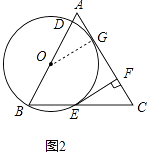
相关试题
