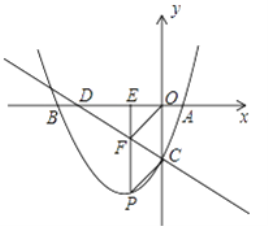
【题目】如图,已知抛物线y=ax2+ ![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣ ![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
(1)试求该抛物线表达式;
(2)求证:点C在以AD为直径的圆上;
(3)是否存在点P使得四边形PCOF是平行四边形,若存在求出P点的坐标,不存在请说明理由。
参考答案:
【答案】(1)y= ![]() x2+
x2+ ![]() x﹣4;(2)见解析;(3)(﹣
x﹣4;(2)见解析;(3)(﹣![]() ,﹣
,﹣![]() )或(﹣8,﹣4).
)或(﹣8,﹣4).
【解析】试题分析:(1)将点A和点C的坐标代入抛物线的解析式可得到关于a、c的方程组,然后解方程组求得a、c的值即可;
(2)求出D点坐标,根据两点间距离公式分别求出AD、AC、CD的长,然后根据勾股定理的逆定理证明出△ADC为直角三角形即可得出结论;
(3)设P(m,![]() m2+
m2+![]() m-4),则F(m,-
m-4),则F(m,-![]() m-4),则PF=-
m-4),则PF=-![]() m2-
m2-![]() m,当PF=OC时,四边形PCOF是平行四边形,然后依据PF=OC列方程求解即可.
m,当PF=OC时,四边形PCOF是平行四边形,然后依据PF=OC列方程求解即可.
试题解析:
(1)解:由题意得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的表达式为y= ![]() x2+
x2+ ![]() x﹣4.
x﹣4.
(2)证明:把y=0代入y=﹣ ![]() x﹣4得:﹣
x﹣4得:﹣ ![]() x﹣4=0,
x﹣4=0,
解得:x=﹣8.
∴D(﹣8,0).
∴OD=8.
∵A(2,0),C(0,﹣4),∴AD=2﹣(﹣8)=10.
由两点间的距离公式可知:AC2=22+42=20,DC2=82+42=80,AD2=100,
∴AC2+CD2=AD2 .
∴△ACD是直角三角形,且∠ACD=90°,
∴点C在以AD为直径的圆上;
(3)解:设P(m, ![]() m2+
m2+ ![]() m﹣4),则F(m,﹣
m﹣4),则F(m,﹣ ![]() m﹣4).
m﹣4).
∴PF=(﹣ ![]() m﹣4)﹣(
m﹣4)﹣( ![]() m2+
m2+ ![]() m﹣4)=﹣
m﹣4)=﹣ ![]() m2﹣
m2﹣ ![]() m.
m.
∵PE⊥x轴,∴PF∥OC.
∴PF=OC时,四边形PCOF是平行四边形.
∴﹣ ![]() m2﹣
m2﹣ ![]() m=4,解得:m=﹣
m=4,解得:m=﹣ ![]() 或m=﹣8.
或m=﹣8.
当m=﹣ ![]() 时,
时, ![]() m2+
m2+ ![]() m﹣4=﹣
m﹣4=﹣ ![]() ,
,
当m=﹣8时, ![]() m2+
m2+ ![]() m﹣4=﹣4.
m﹣4=﹣4.
∴点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )或(﹣8,﹣4).
)或(﹣8,﹣4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
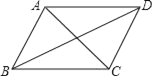
A. 当AB=BC时四边形ABCD是菱形
B. 当AC⊥BD时四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD且∠ABC=90°时四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.
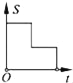 B.
B. 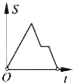 C.
C. 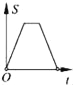 D.
D. 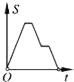
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=8,AC=6,M为BC上的一动点,ME⊥AB于E,MF⊥AC于F,N为EF的中点,则MN的最小值为( )
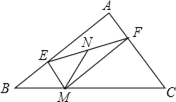
A. 4.8B. 2.4C. 2.5D. 2.6
-
科目: 来源: 题型:
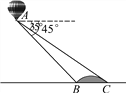
查看答案和解析>>【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈
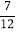 ,cos35°≈
,cos35°≈ ,tan35°≈
,tan35°≈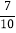 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
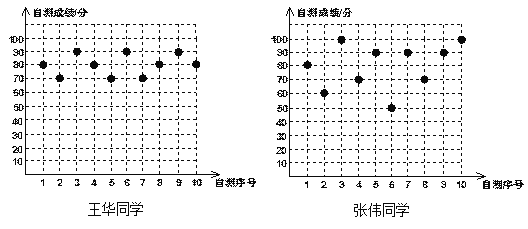
(1)根据上图中提供的数据列出如下统计表:
平均成绩(分)
中位数(分)
众数(分)
方差(S2)
王华
80
b
80
d
张伟
a
85
c
260
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在以点O为原点的数轴上,点A表示的数是3,点B在原点的左侧,且AB=6AO(我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB).
(1)B点表示的数是_______.
(2)若动点P从O点出发,以每秒2个单位长度的速度匀速向左运动,问经过几秒钟后PA=3PB?并求出此时P点在数轴上对应的数.
(3)若动点M.P.N分别同时从A、O、B出发,匀速向右运动,其速度分别为1个单位长度/秒.2个单位长度/秒.4个单位长度/秒,设运动时间为t秒,请直接写出PM.PN.MN中任意两个相等时的时间.

相关试题

