【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A. 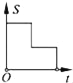 B.
B. 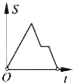 C.
C. 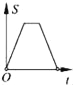 D.
D. 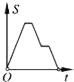
参考答案:
【答案】D
【解析】
根据点P在AD、DE、EF、FG、GB上时,△ABP的面积S与时间t的关系确定函数图象.
当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时
间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小
而减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减
小而减小;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一对数,如下表,第
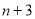 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)第1个
第2个
第3个
第4个
第5个
……
a
b
c
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.(1)直接写出
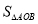 = ;
= ;(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线
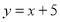 于点P,求点P的坐标.
于点P,求点P的坐标.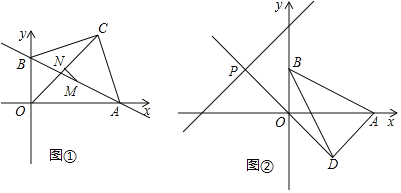
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
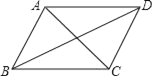
A. 当AB=BC时四边形ABCD是菱形
B. 当AC⊥BD时四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD且∠ABC=90°时四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=8,AC=6,M为BC上的一动点,ME⊥AB于E,MF⊥AC于F,N为EF的中点,则MN的最小值为( )
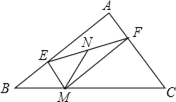
A. 4.8B. 2.4C. 2.5D. 2.6
-
科目: 来源: 题型:
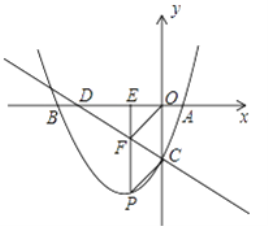
查看答案和解析>>【题目】如图,已知抛物线y=ax2+
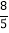 x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣  x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+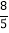 x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.(1)试求该抛物线表达式;
(2)求证:点C在以AD为直径的圆上;
(3)是否存在点P使得四边形PCOF是平行四边形,若存在求出P点的坐标,不存在请说明理由。
-
科目: 来源: 题型:
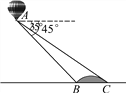
查看答案和解析>>【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈
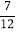 ,cos35°≈
,cos35°≈ ,tan35°≈
,tan35°≈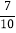 )
)
相关试题

