【题目】先化简,再求值: ![]() ,其中x的值从不等式组
,其中x的值从不等式组![]() 的整数解中选取.
的整数解中选取.
参考答案:
【答案】-2.
【解析】将原式括号中找出两分母的最简公分母,通分并利用同分母分式的减法法则计算,分子进行合并整理,同时将除式的分母利用公式分解因式,然后利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分后即可得到结果,分别求出x满足的不等式组两个一元一次不等式的解集,找出两解集的公共部分确定出不等式组的解集,在解集中找出整数解,即为x的值,将x的值代入化简后的式子中计算,即可得到原式的值.
原式
![]() .
.
解不等式组![]() ,得
,得![]() ≤
≤![]() <
<![]() .
.
∴不等式组的整数解为-1,0,1,2.
若使分式有意义,只能取![]() .
.
∴原式![]()
“点睛”此题考查了分式的化简求值,以及一元一次不等式的解法,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母是多项式,应先将多项式分解因式后再约分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生某月有零花钱a元,其支出情况如图所示,那么下列说法不正确的是( )
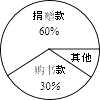
A.该学生捐赠款为0.6a元
B.捐赠款所对应的圆心角为240°
C.捐赠款是购书款的2倍
D.其他消费占10% -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
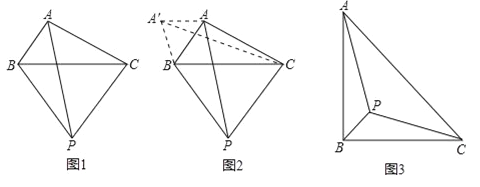
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
A.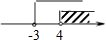
B.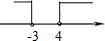
C.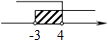
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2x﹣9=5x+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
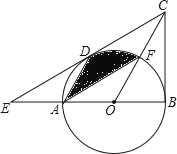
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1 , A2 , A3 , A4 , …表示,则顶点A55的坐标是( )
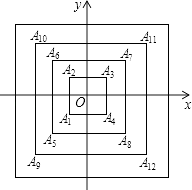
A.(13,13)
B.(﹣13,﹣13)
C.(14,14)
D.(﹣14,﹣14)
相关试题

