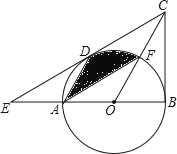
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.
(2)首先证明S阴=S扇形ODF,然后利用扇形面积公式计算即可.
试题解析:(1)证明:连接OD,与AF相交于点G,∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,∵AD∥OC,∴∠ADO=∠1,∠DAO=∠2,∵OA=OD,∴∠ADO=∠DAO,∴∠1=∠2,在△CDO和△CBO中,∵CO=CO,∠1=∠2,OD=OC,∴△CDO≌△CBO,∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,∵∠ECB=60°,∴∠3=![]() ∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=
∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=![]() =
= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
A.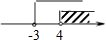
B.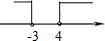
C.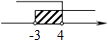
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
 ,其中x的值从不等式组
,其中x的值从不等式组 的整数解中选取.
的整数解中选取. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2x﹣9=5x+3.
-
科目: 来源: 题型:
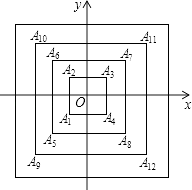
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1 , A2 , A3 , A4 , …表示,则顶点A55的坐标是( )
A.(13,13)
B.(﹣13,﹣13)
C.(14,14)
D.(﹣14,﹣14) -
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个两根分别为0和2的一元二次方程:___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年第一季度,泰州市共完成工业投资22300000000元,22300000000这个数可用科学记数法表示为 .
相关试题

