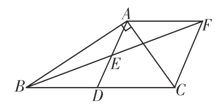
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用平行线的性质及中点的定义,可利用AAS证得结论;
(2)由(1)可得AF=BD,结合条件可求得AF=DC,则可证明四边形ADCF为平行四边形,再利用直角三角形的性质可证得AD=CD,可证得四边形ADCF为菱形;
证明:(1)∵AF∥BC
∴∠AFE=∠DBE
∵E是AD中点,
∴AE=DE
在△AEF和DEB中
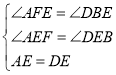
∴△AEF≌△DEB(AAS)
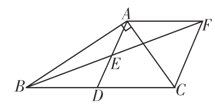
(2)在Rt△ABC中,D是BC的中点,
所以,AD=BD=CD
又AF∥DB,且AF=DB,
所以,AF∥DC,且AF=DC,
所以,四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批西服,进价为每套250元,原定每套以290元的价格销售,这样每天可销售200套.如果每套比原销售价降低10元销售,则每天可多销售100套.该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论(每套西服的利润=每套西服的销售价﹣每套西服的进价).
(1)按原销售价销售,每天可获利润 元.
(2)若每套降低10元销售,每天可获利润 元.
(3)如果每套销售价降低10元,每天就多销售100套,每套销售价降低20元,每天就多销售200套.
按这种方式:
①若每套降低10x元,则每套的销售价格为 元;(用代数式表示)
②若每套降低10x元,则每天可销售 套西服.(用代数式表示)
③若每套降低10x元,则每天共可以获利润 元.(用代数式表示)
-
科目: 来源: 题型:
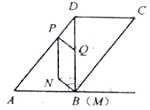
查看答案和解析>>【题目】如图,BD是□ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD—DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),□PQMN与□ABCD重叠部分图形的面积为S(cm2).
(1)AP=_______cm(同含t的代数式表示).
(2)当点N落在边AB上时,求t的值.
(3)求S与t之间的函数关系式.
(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用平面截掉一个长方体的一个角(即切去一个三棱锥),则剩下的几何体最多有_____顶点,最少有_____条棱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣12)﹣(﹣
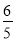 )+(﹣8)﹣
)+(﹣8)﹣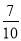
(2)15﹣8÷(﹣2)×
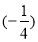
(3)0﹣23+(﹣4)3﹣
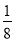
(4)(﹣3)2×
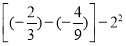
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,过抛物线
 与y轴的交点作y轴的垂线,则称这条垂线是该抛物线的伴随直线.例如:抛物线
与y轴的交点作y轴的垂线,则称这条垂线是该抛物线的伴随直线.例如:抛物线 的伴随直线为直线
的伴随直线为直线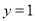 .抛物线
.抛物线 的伴随直线l与该抛物线交于点A、D(点A在y轴上),该抛物线与x轴的交点为B(-1,0)和C(点C在点B的右侧).
的伴随直线l与该抛物线交于点A、D(点A在y轴上),该抛物线与x轴的交点为B(-1,0)和C(点C在点B的右侧).(1)若直线l是y=2,求该抛物线对应的函数关系式.
(2)求点D的坐标(用含m的代数式表示).
(3)设抛物线
 的顶点为M,作OA的垂直平分线EF,交OA于点E,交该抛物线的对称轴于点F.
的顶点为M,作OA的垂直平分线EF,交OA于点E,交该抛物线的对称轴于点F.①当△ADF是等腰直角三角形时,求点M的坐标.
②将直线EF沿直线l翻折得到直线GH,当点M到直线GH的距离等于点C到直线EF的距离时,直接写出m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】晨光文具店的某种毛笔每支售价30元,书法纸每本售价10元.为促销制定了两种优惠方案:甲方案,买一支毛笔就送一本书法纸;乙方案,按购买的总金额打8折.某校欲为书法小组购买这种毛笔10支,书法纸x(x≥10)本.
(1)求甲方案实际付款金额
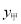 元与x的函数关系式和乙方案实际付款金额
元与x的函数关系式和乙方案实际付款金额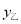 元与x的函数关系式;
元与x的函数关系式;(2)试通过计算为该校提供一种节约费用的购买方案.
相关试题

