【题目】晨光文具店的某种毛笔每支售价30元,书法纸每本售价10元.为促销制定了两种优惠方案:甲方案,买一支毛笔就送一本书法纸;乙方案,按购买的总金额打8折.某校欲为书法小组购买这种毛笔10支,书法纸x(x≥10)本.
(1)求甲方案实际付款金额![]() 元与x的函数关系式和乙方案实际付款金额
元与x的函数关系式和乙方案实际付款金额![]() 元与x的函数关系式;
元与x的函数关系式;
(2)试通过计算为该校提供一种节约费用的购买方案.
参考答案:
【答案】(1)y甲=10x+200(x≥10);![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)甲方案实际付款=10支毛笔的价钱+10本以外练习本的总价钱,把相关数值代入即可求解;乙方案实际付款=(10支毛笔的总价钱+练习本的总价钱)×0.8,把相关数值代入即可求解;
(2)把①②得到的式子比较大小列出式子计算即可.
解:(1)①![]() =30×10+10(x-10)=10x+200(x≥10);
=30×10+10(x-10)=10x+200(x≥10);
②![]() =(30×10+10x)×0.8=8x+240;
=(30×10+10x)×0.8=8x+240;
(2)①∵10x+200>8x+240,
解得:x>20;
∴当练习本超过20本时,选择乙方案;
②∵10x+200=8x+240,
解得:x=20;
∴当练习本为20本时,两种方案价钱一样;
③∵10x+200<8x+240,
解得:x<20;
∴当练习本少于20本时,选择甲方案.
答:当练习本超过20本时,选择乙方案;当练习本为20本时,两种方案价钱一样;当练习本少于20本时,选择甲方案.
-
科目: 来源: 题型:
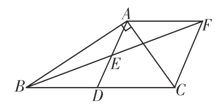
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣12)﹣(﹣
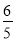 )+(﹣8)﹣
)+(﹣8)﹣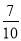
(2)15﹣8÷(﹣2)×
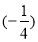
(3)0﹣23+(﹣4)3﹣
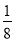
(4)(﹣3)2×
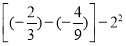
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,过抛物线
 与y轴的交点作y轴的垂线,则称这条垂线是该抛物线的伴随直线.例如:抛物线
与y轴的交点作y轴的垂线,则称这条垂线是该抛物线的伴随直线.例如:抛物线 的伴随直线为直线
的伴随直线为直线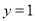 .抛物线
.抛物线 的伴随直线l与该抛物线交于点A、D(点A在y轴上),该抛物线与x轴的交点为B(-1,0)和C(点C在点B的右侧).
的伴随直线l与该抛物线交于点A、D(点A在y轴上),该抛物线与x轴的交点为B(-1,0)和C(点C在点B的右侧).(1)若直线l是y=2,求该抛物线对应的函数关系式.
(2)求点D的坐标(用含m的代数式表示).
(3)设抛物线
 的顶点为M,作OA的垂直平分线EF,交OA于点E,交该抛物线的对称轴于点F.
的顶点为M,作OA的垂直平分线EF,交OA于点E,交该抛物线的对称轴于点F.①当△ADF是等腰直角三角形时,求点M的坐标.
②将直线EF沿直线l翻折得到直线GH,当点M到直线GH的距离等于点C到直线EF的距离时,直接写出m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将有规律的整数1,﹣2,3,﹣4,5,﹣6,…按照如图所示的方式排成数阵.
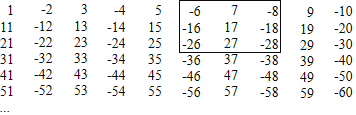
(1)用字母表示如图横行任意三个相邻的数的关系 、 、 .
(2)如图,方框中九个数之和与正中间数17有什么关系?请计算说明.
(3)用这样的方框在数阵中移动(一直保持框出数阵中的9个数),那么方框中九个数之和与正中间数关系,还如(2)中一样成立吗?请用字母解释其中所包含的规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,
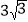 ),反比例函数
),反比例函数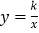 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A.
 B. -
B. - C.
C. 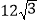 D. -
D. -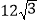
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)-7x+2 = 2x-4 (2)2(x-2)- 6(x-1)= 3(1+x)
(3)
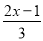 ﹣
﹣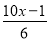 =1 (4)
=1 (4) .
.
相关试题

