【题目】某商场购进一批西服,进价为每套250元,原定每套以290元的价格销售,这样每天可销售200套.如果每套比原销售价降低10元销售,则每天可多销售100套.该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论(每套西服的利润=每套西服的销售价﹣每套西服的进价).
(1)按原销售价销售,每天可获利润 元.
(2)若每套降低10元销售,每天可获利润 元.
(3)如果每套销售价降低10元,每天就多销售100套,每套销售价降低20元,每天就多销售200套.
按这种方式:
①若每套降低10x元,则每套的销售价格为 元;(用代数式表示)
②若每套降低10x元,则每天可销售 套西服.(用代数式表示)
③若每套降低10x元,则每天共可以获利润 元.(用代数式表示)
参考答案:
【答案】(1)8000,(2)9000;(3)①290﹣10x,②200+100x,③(40﹣10x)(200+100x).
【解析】
(1)根据利润=每件的获利×件数,利用(290﹣250)×200算出即可;
(2)根据利润=每件的获利×件数,利用(280﹣250)×(200+100)算出即可;
(3)①根据每套降低10x元,每套的销售价格为:(290﹣10x)元,
②每套降低10x元,每天可销售(200+![]() )套西服求出即可.
)套西服求出即可.
③依据利润=每件的获利×件数,即可解决问题.
根据题意得:
依据利润=每件的获利×件数,
(1)(290﹣250)×200=8000(元),
(2)(280﹣250)×(200+100)=9000(元),
(3)①∵每套降低10x元,∴每套的销售价格为:(290﹣10x)元,
②∵每套降低10x元,∴每天可销售(200+100x)套西服.
③∵每套降低10x元,
∴每套的利润为:(290﹣10x﹣250)=(40﹣10x)元,
每天可销售(200+100x)套西服.
(40﹣10x)(200+100x),
每天共可以获利润为:(40﹣10x)(200+100x).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD的中点,则四边形EFGH的形状一定是( )
A. 平行四边形B. 矩形C. 菱形D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减(辆)
-1
+3
-2
-4
+7
-5
-10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
-
科目: 来源: 题型:
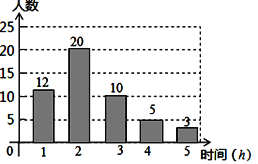
查看答案和解析>>【题目】珠海市某中学在创建“书香校园”活动中,为了解学生的读书情况,某校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
(1)被抽查学生阅读时间的中位数为 h,平均数为 h;
(2)若该校共有1500名学生,请你估算该校一周内阅读时间不少于3h的学生人数.
-
科目: 来源: 题型:
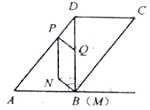
查看答案和解析>>【题目】如图,BD是□ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD—DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),□PQMN与□ABCD重叠部分图形的面积为S(cm2).
(1)AP=_______cm(同含t的代数式表示).
(2)当点N落在边AB上时,求t的值.
(3)求S与t之间的函数关系式.
(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用平面截掉一个长方体的一个角(即切去一个三棱锥),则剩下的几何体最多有_____顶点,最少有_____条棱.
-
科目: 来源: 题型:
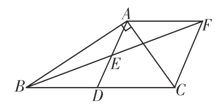
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
相关试题

