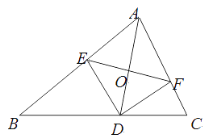
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
A. ②③ B. ②④ C. ①②③ D. ②③④
参考答案:
【答案】D
【解析】
由AD是角平分线及DE、DF均为高可知△AED≌△AFD,则可得AE=AF,DE=DF,继而得到AD是EF的垂直平分线,由此可判断②和③正误,再由勾股定理可判断④的正误,而①的结论无法由已知条件推出.
解:∵AD是角平分线,
∴∠EAD=∠FAD,
∵∠AED=∠AFD=90°,AD=AD,
∴△ADE≌△AFD,
∴AE=AF,DE=DF,
∴AD⊥EF,②正确,
∵∠BAC=90°,∠AED=∠AFD=90°
又∵AE=AF,
∴四边形AEDF是正方形,③正确,
∵∠AED=∠AFD=90°,
∴AE2+DE2=AF2+DF2=AD2
∵DE=DF,
∴AE2+DF2=AF2+DE2,④正确.
根据前述已得结论,需要四边形AEDF是菱形才能得到OA=OD的结论,而题干并未给出这个条件,①错误,
故选择D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价7元售出150本时,出现滞销,便以定价的5折售完剩余的书.
(1)每本书第一次的批发价是多少钱?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则
 的值是( )
的值是( )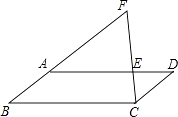
A.
B.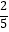
C.
D.
-
科目: 来源: 题型:
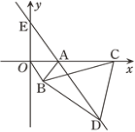
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边三角形△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化,请说明理由.
(3)当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在CB上的A′处,折痕CD,则∠A′DB= ( )
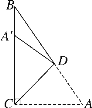
A. 10° B. 20° C. 30° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2
 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:

表2:四个家庭2017年的年用水量和缴纳水费情况:
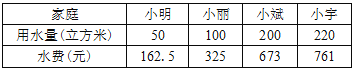
请你根据表1、表2提供的数据回答下列问题:
(1)表1中的
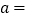 __________,
__________,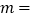 _____________;
_____________;(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?
相关试题

